Numericka kvadratura a hodnoty bazovych funkci

Integral pres polygonalni oblast $\Omega_\Delta \approx \Omega$ (v pripade polygonalni oblasti ke $\Omega_\Delta \equiv \Omega$). Dale pouzijeme triangulaci oblasti $\Omega_\Delta$ pomoci trojuhelnikovych prvku

$$\overline{\Omega_\Delta } = \bigcup\limits_{K\in \tau_\Delta } K$$

a tedy integraci pres oblast $\Omega$ lze nahradit integraci pres vsechny trojuhelnikove prvky

$$\int_{\Omega_\Delta } f(x)\, dx = \sum_{K \in \tau_\Delta } \int_K f(x)\, dx,$$

a integral pres jednotlive prvky jsou pak transformovany na referencni trojuhelnik pomoci linearniho zobrazeni

$$F_K: \hat{K} \mapsto K , \qquad \qquad x = F_K(\hat{x}) = {\cal B} \hat{x} + {\mathbf b}.$$

Pro linearniho zobrazeni $F_K$ plati navic det ${\cal B} = \vert F_K^\prime\vert = meas(K)$. V pripade pouziti izoparametrickych konecnych prvku bude situace ponekud komplikovanejsi (zobrazeni $F_K$ nebude linearni). Podle vety o substituci pak plati

$$\int_K f(x) dx = \int_{\hat{K}} f\Bigl(F_K(\hat{x})\Bigr) \vert F_K^\prime\vert d\hat{x}$$

a pouzijeme-li kvadraturni vzorec dostaneme

$$\int_K f(x) dx = \int_{\hat{K}} f\Bigl(F_K(\hat{x})\Bigr) \vert F... ... \approx \frac{\vert K\vert}{2} \cdot \sum_{m=1}^{n_2} w_m \cdot f(\hat{x}_m),$$

kde $w_m$ jsou vahy kvadratury (data ulozena v poli w2[0..n2]) a $\hat{x}_m$ jsou kvadraturni uzly (uzly ulozeny pomoci barycentrickych souradnic v poli L[0..2][0..n2]). Kvadratura je konstruovana tak aby byla presna pro polynomy stupne mene nebo rovno q2. Uchovany jsou dve verze kvadratury, druha v W2[], L1[][], Q2- stupen polynomu, N2 - pocet uzlu.

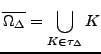
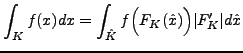
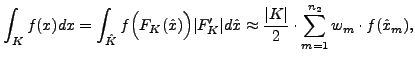
Dale je nutne pocitat hranicni integraly. Uvazujeme-li $\int_{\Gamma_O} g(x) dS$ lze ho zapsat nasledovne

$$\int_{\Gamma_O} g(x) dS = \sum_{S\in s_{\Gamma_O}} \int_S g(x) dS$$

a integral pres stranu trojuhelniku S lze transformovat na interval $\hat{S}=\langle 0 , 1 \rangle$ a

$$\int_S g(x) dS = \int_{\hat{S}} g(F_{K_S}(\hat{x})) d\hat{S} \approx \sum_{m=1}^{n_1} w_m^{\hat{S}} \cdot g(F_{K_S}(\hat{x}_{\hat{S},m})).$$

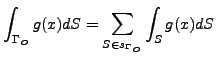
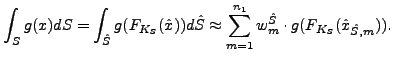
/* Quadrature formulae */
/* varianta A */
int q1=0,q2=0;  /* polynomial degree */
int n1=0,n2=0;  /* number of q.nodes */
double *X=NULL,*w=NULL; /* 1dimensional quadrature formula */
double **L=NULL,*w2=NULL; /* 2dimensional q.f. */
/* varianta B */
int Q1=0,Q2=0;  /* polynomial degree */
int N1=0,N2=0;  /* number of q.nodes */
double *X1=NULL,*W=NULL;        /* 1dimensional quadrature formula */
double **L1=NULL,*W2=NULL;      /* 2dimensional q.f. */