=1.000000pt

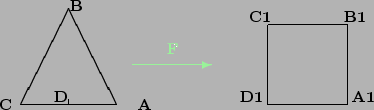
Dale ctverec (![]() ) s vrcholy
) s vrcholy ![]() ,
, ![]() ,
, ![]() ,
,
![]() . Bilinearni zobrazeni
. Bilinearni zobrazeni ![]() transformujici obdelnik/ctverec
transformujici obdelnik/ctverec ![]() na trojuhelnik
na trojuhelnik ![]() pak lze definovat tak, aby mapovalo body A1 na A, B1 na B,
C1 na C a D1 na D. Tedy
pak lze definovat tak, aby mapovalo body A1 na A, B1 na B,
C1 na C a D1 na D. Tedy
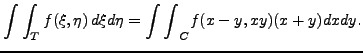
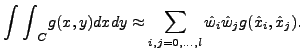
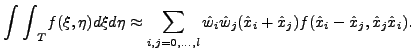
V nasem pripade pouzivame jako referencni element trojuhelnik ![]() s body
oznacenymi jakozto
s body
oznacenymi jakozto
![]() . Trojuhelnik
. Trojuhelnik ![]() lze
zobrazit na
lze
zobrazit na ![]() pomoci linearniho zobrazeni
pomoci linearniho zobrazeni
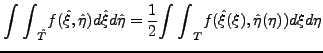
Hodnoty na referencnim trojuhelniku ![]() jsou definovany v uzlech
kvadratury. Hodnoty jsou definovany pomoci barycentrickych souradnic
jsou definovany v uzlech
kvadratury. Hodnoty jsou definovany pomoci barycentrickych souradnic
![]() a
a ![]() . Razeni bazovych funkci je nasledovne pro trojuhelnik
o vrcholech ABC: node(A), node(B), node(C), side(AB), side(BC), side(CA), bubble(ABC).
. Razeni bazovych funkci je nasledovne pro trojuhelnik
o vrcholech ABC: node(A), node(B), node(C), side(AB), side(BC), side(CA), bubble(ABC).
Bazova funkce definovana na referencnim trojuhelniku
lze zderivovat, ovsem jeji derivace zavisi na deformaci trojuhelniku. Hodnoty na trojuhelniku (v integracnich bodech) jsou uschovany v promenne basefn_values. Na strane v promenne side_basefn_values. Derivace (prvni a druhe) podle barycentrickych souradnic jsou uschovany v promennych grad_basefn_values[0..2] a hes_basefn_values[0..2][0..2].
double **basefn_values=NULL; double **sidebasefn_values=NULL; double **grad_basefn_values[3]; double **hes_basefn_values[3][3]; int *base_pressure_idx=NULL; |
Indexovani promennych je uvedeno zde:
I ... INDEX BAZOVE FUNKCE M ... INDEX BODU NUMERICKE KVADRATURY basefn_values [I][M] grad_basefn_values[DERIVACE][I][M] hes_basefn_values [DERIVACE][DERIVACE][I][M] |