|
Data Structures |
| struct | matrix |
| void | add_mat (matrix A, const matrix B) |
| void | construct_mat (matrix *A, long n, long m) |
| void | construct_mat_copy (matrix *A, const matrix B) |
| void | construct_mat_multiply (matrix *out, const matrix A, const matrix B) |
| void | construct_mat_transpose (matrix *out, const matrix in) |
| void | destruct_mat (matrix *A) |
| void | ludcmp (matrix out) |
| void | lusolve (vector sol, const matrix out, const vector rhs) |
| void | mat_transf (matrix out, long ia, long ib, long ic, double *_x, double *_y) |
| void | mat_transfinv (matrix out, long ia, long ib, long ic, double *_x, double *_y) |
| void | matrix_multiply_left (vector out, const vector v, const matrix A) |
| void | matrix_multiply_mat (matrix *out, const matrix A, const matrix B) |
| void | matrix_multiply_right (vector out, const matrix A, const vector v) |
| void | matrix_reziduum (vector out, const matrix A, const vector v) |
| void | multiply_mat (matrix M, const double beta) |
| void | multiply_mat_rows (matrix A, const vector v) |
| void | save_mat (const matrix which, char *filename) |
| void | solve_mat (vector sol, const matrix A, const vector b) |
| void | subtract_mat (matrix A, const matrix B) |
| void | transpose_mat (matrix *out, const matrix in) |
| void | upper_solve_mat (vector out, const matrix R, const vector b, long k) |
| void | zeroize_mat (matrix A) |
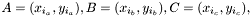 .
. the matrix of linear transformation
the matrix of linear transformation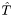 onto triangle
onto triangle 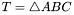 .
.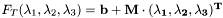
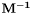 .
. 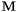 , i.e.
, i.e. 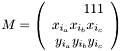
 1.4.6
1.4.6