Triangulation

In order to define the space of finite elements a triangulation of the computational domain $\Omega$ is needed. In the practical implementation the triangulation is provided from an external file (triangulation file). Program FEMFLUID can use two input formats. Recently, FEMFLUID uses mesh format defined by the automatic anisotropic mesh generator ANGENER (V.Dolejsi, MFF UK, Praha). The format of the input file then reads (in FEMFLUID the second line is ignored - in ANGENER used for periodical boundary)

$$ $Header$

$$\quad Points \left\{ \begin{array}{c} \\ \\ \\ \\ \end{array}\right.$$

$$Elements \left\{ \begin{array}{c} \\ \\ \\ \\ \\ \\ \end{array}\right.$$

$$\quad BSides \left\{ \begin{array}{c} \\ \\ \\ \\ \\ \\ \end{array}\right.$$

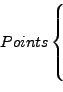
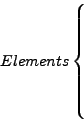
#Points #Elements #BoundarySides #Marks
0.0 0.0 0 0 0.0 0.0 0 0
PointX(1)           PointY(1)
PointX(2)           PointY(2)
.                   .
.                   .
.                   .
PointX(#Points)     PointY(#Points)
ElementI(1)         ElementJ(1)         ElementK(1)
ElementI(2)         ElementJ(2)         ElementK(2)
ElementI(3)         ElementJ(3)         ElementK(3)
.                   .
.                   .
.                   .
ElementI(#Elements) ElementJ(#Elements) ElementK(#Elements)
BndrSideI(1)        BndrSideJ(1)        BndrMARK(1)
BndrSideI(2)        BndrSideJ(2)        BndrMARK(2)
BndrSideI(3)        BndrSideJ(3)        BndrMARK(3)
.                   .
.                   .
.                   .
BndrSideI(#BSides)  BndrSideJ(#BSides)  BndrMARK(#BSides)

The orientation of triangles needs to be chosen in the standard way. The orientation of boundary sides needs to preserve the orientation of the adjacent triangle, i.e. that the computational domain should be on the left hand side from the oriented boundary side.

Figure 1: Triangulation with 8th points, 8th elements and 8th boundary sides.

Triangulation can be also read from files generated by the program TRIANGLE (optional, program changes needed).

The triangulation from Figure 1 is described with the following triangulation file

7 6 6 4
0.0 0.0 0 0 0.0 0.0 0 0
0.0 0.0
1.0 1.0
1.0 0.0
0.0 0.5
0.5 0.5
0.0 1.0
0.5 1.0
1 3 5 
3 2 5
5 2 7
1 5 4
4 5 6
5 7 6
1 3 10
3 2 20
2 7 60
7 6 60
6 4 1
4 1 1