Konstruktivní geometrie 2023/24
Rozvinutelné plochy
Rozvinutelnost
Plocha je rozvinutelná do roviny právě tehdy, když existuje tzv. isometrické zobrazení této plochy do roviny, tj. zobrazení zachovávající délky oblouků a úhly křivek.
Podmínky rozvinutelnosti:
- plocha je přímková
- podél celé každé povrchové přímky existuje jediná tečná rovina
Podmínky rozvinutelnosti

válcová plocha

Převzato z přednášek ZČU v Plzni
kuželová plocha
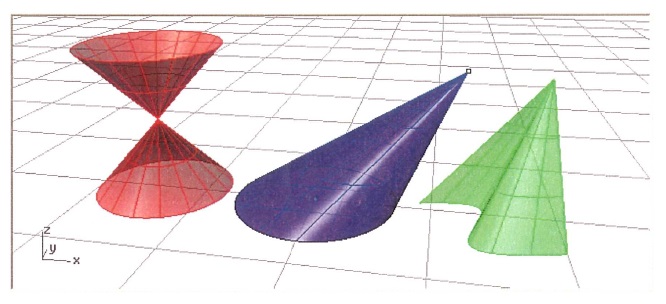
převzato z přednášek ZČU v Plzni
plocha tečen prostorové křivky
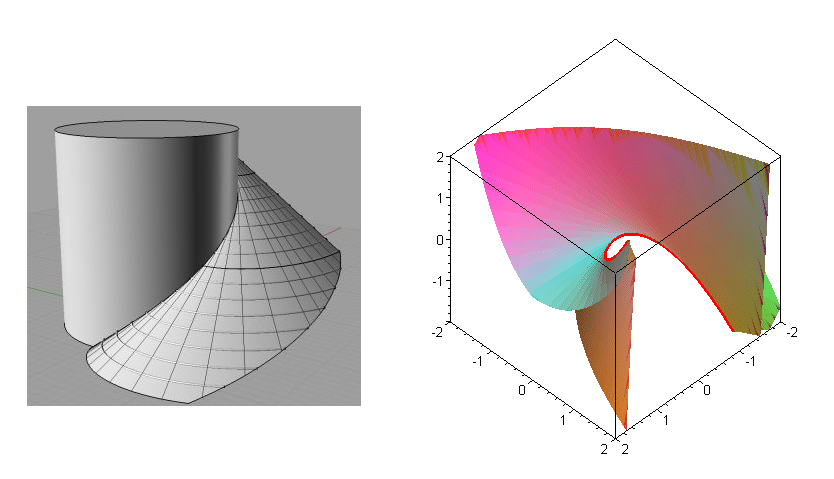
Převzato z mathcurve.com - plocha tečen šroubovice a plocha tečen "prostorové" paraboly
přechodová rozvinutelná plocha

Plocha válcová
Princip rozvinutí
- válcovou plochu nahradit pláštěm vepsaného hranolu
- sestrojit síť hranolu - rozvíjet podél křivky normálového řezu!
- lomené čáry podstav nahradit hladkými křivkami
Příklad 1 (list 85): Rozviňte část válcové plochy mezi kružnicí $k$ a elipsou $l$ v rovině $\rho$.

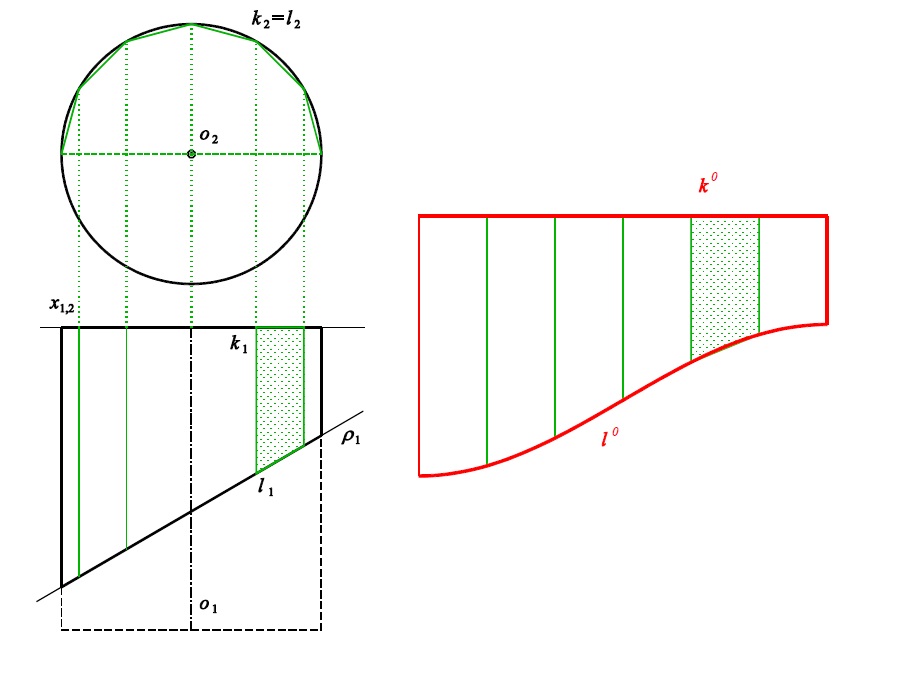
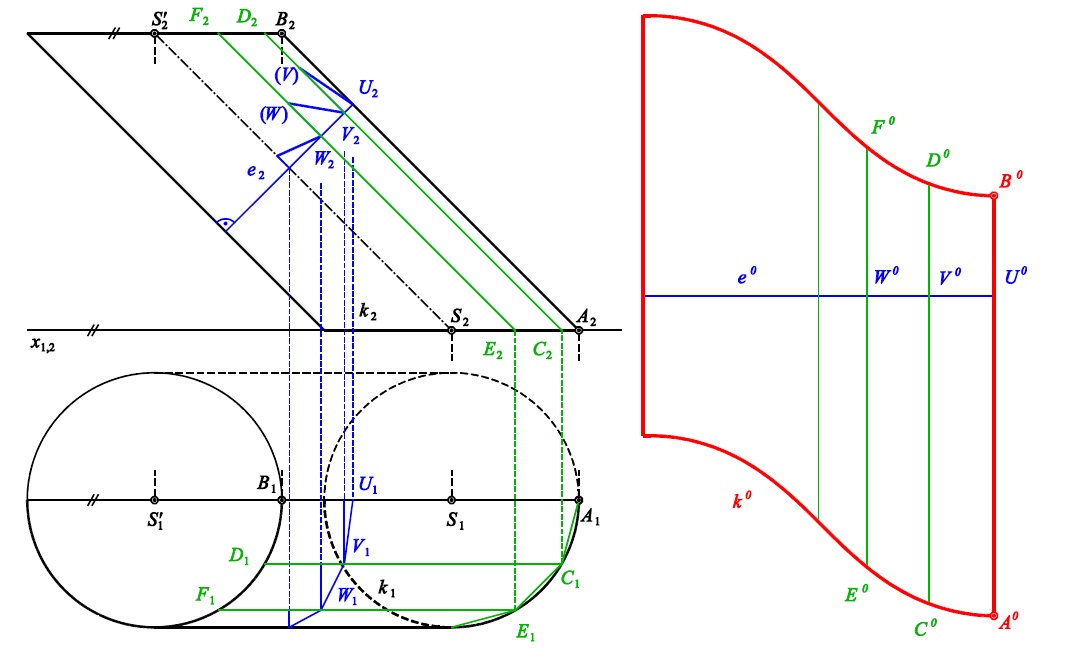
Příklad 2 (list 91): Rozviňte přední polovinu pláště kosého kruhového válce mezi podstavou $k$ a $k'$
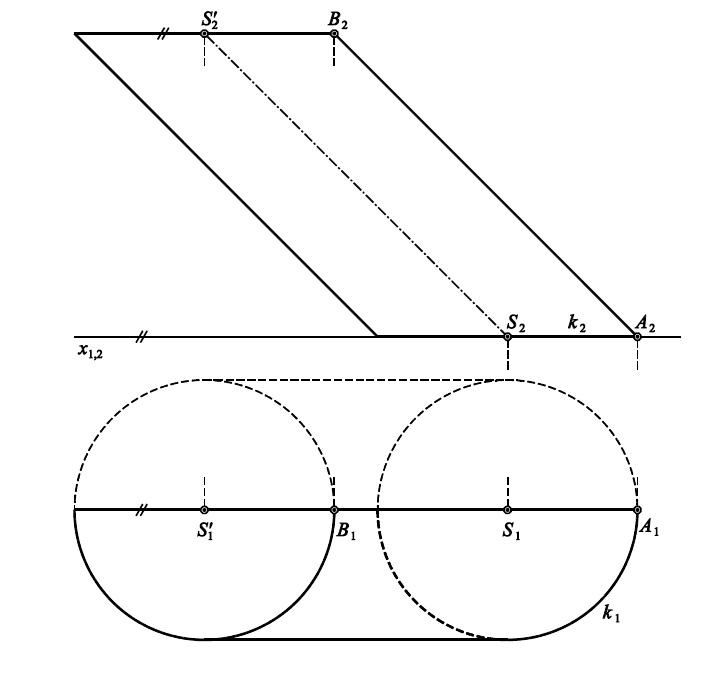
Plocha kuželová
Princip rozvinutí
- kuželovou plochu nahradit vepsaným jehlanem
- sestrojit síť jehlanu
- lomenou čáru podstavy nahradit hladkou křivkou
Příklad 3 (list 86): Rozviňte část kuželové plochy mezi podstavou $k$ a elipsou $l$ v rovině $\rho$.
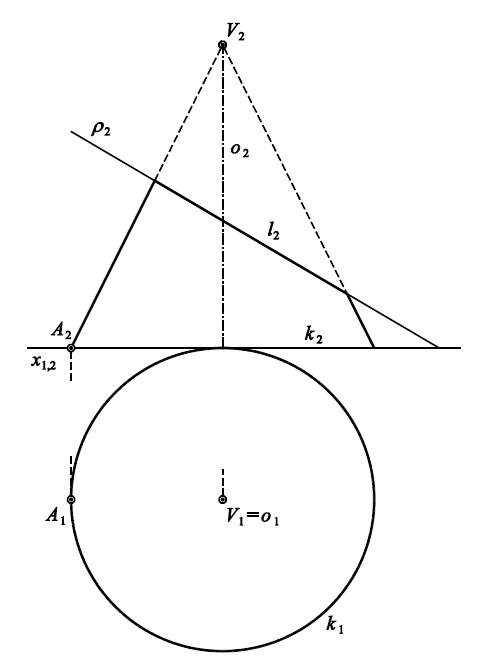
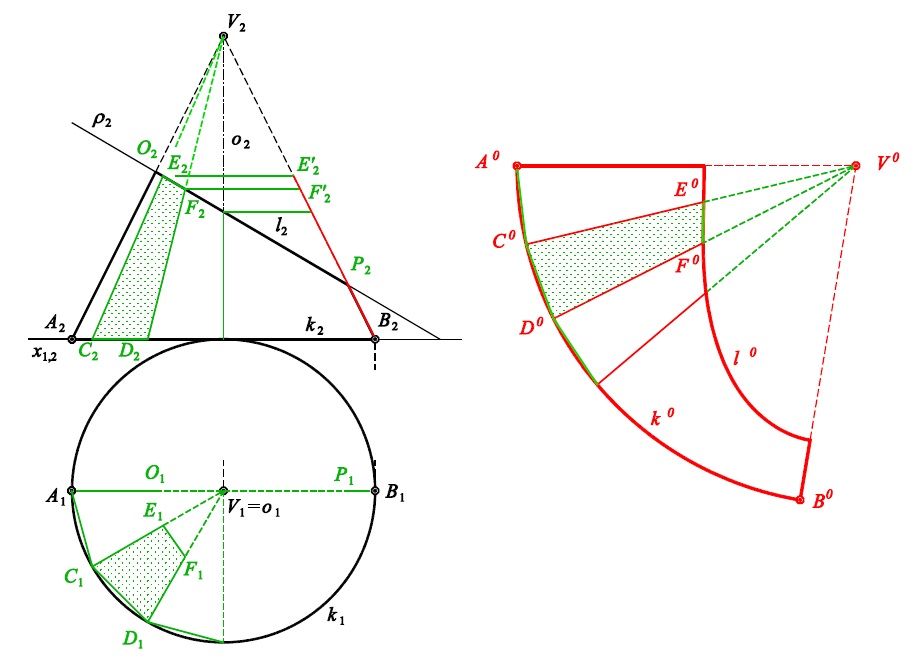
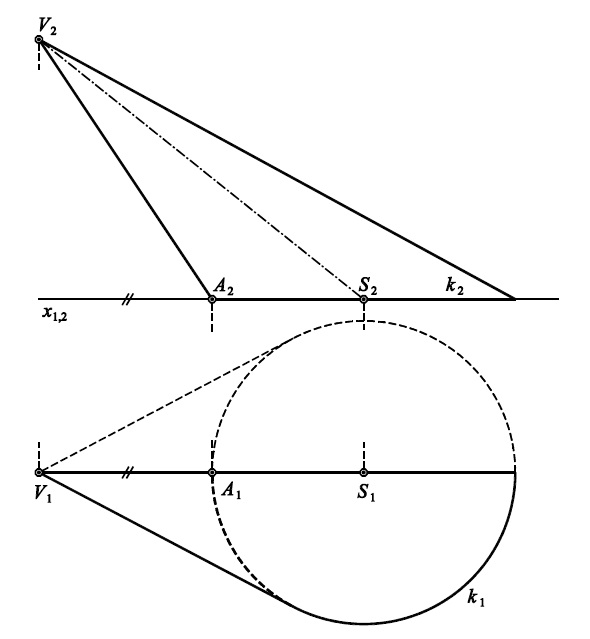
Příklad 4 (list 92): Rozviňte přední polovinu pláště kosého kruhového kužele $(V,k)$.

Plocha tečen šroubovice (*)
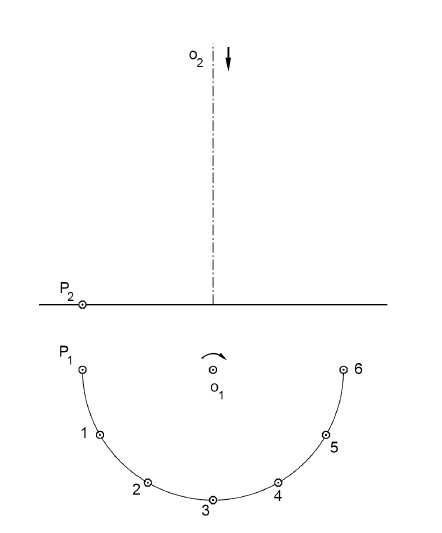
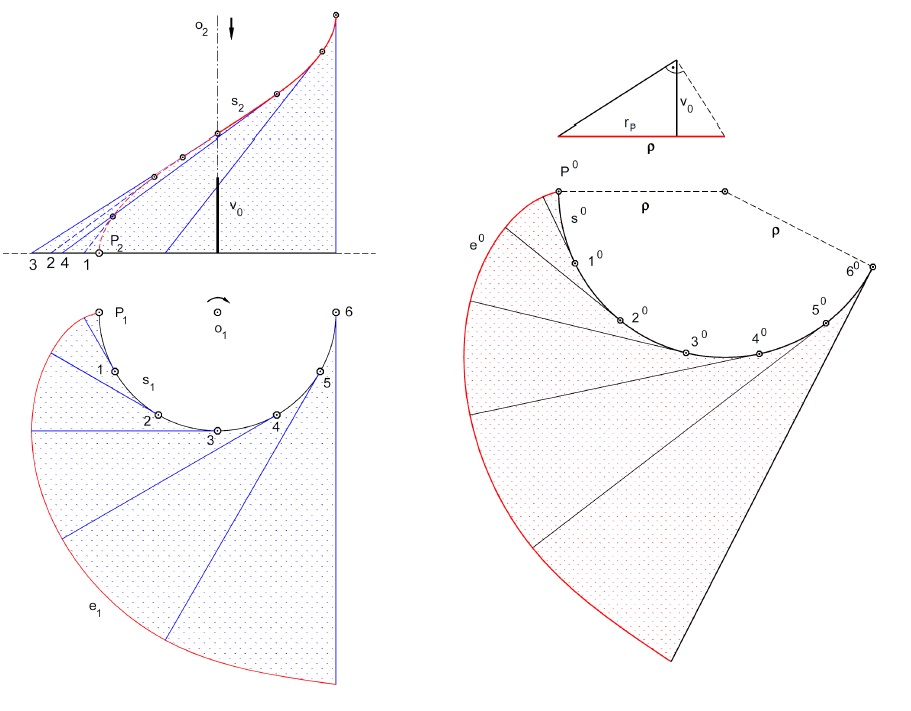
Příklad 5: Je dána šroubovice ($P, o, v = 120$, pravotočivá). Sestrojte nárys poloviny závitu.
V zobrazených bodech sestrojte tečny šroubovice omezené dotykovým bodem a půdorysnou. Tuto část plochy tečen šroubovice rozviňte do roviny.
Odkazy na další materiály
- kapitola z elektronických skript (doc. Linkeová)
- prezentace z přednášky KMA ZČU v Plzni
příště: