Počítačová grafika 2022/23

Plochy

Příklad

Bézierova plocha $P$ je dána mapou
\[ M_P = \begin{pmatrix} (0,0,20) & (0,10,20) & (0,20,10) & (0,30,10) \\ (10,0,5) & (10,10,0) & (10,20,5) & (10,30,5) \\ (20,0,0) & (20,10,0) & (20,20,5) & (20,30,0) \end{pmatrix} \]
Určete mapu $M_R$ Bézierovy plochy $R$, která je napojena k ploše $P$ podél okraje $P_0(u)$ se spojitostí $C^0$.
Určete mapu $M_S$ Bézierovy plochy $S$, která je napojena k ploše $P$ podél okraje $P_1(v)$ se spojitostí $C^1$.
Určete mapu $M_T$ Bézierovy plochy $T$, která je napojena k ploše $P$ podél okraje $P_1(u)$ se spojitostí $C^2$.
Všechny plochy jsou stejného typu, z-ové souřadnice bodů, které neovlivní danou spojitost volte nulové.
Plát P:
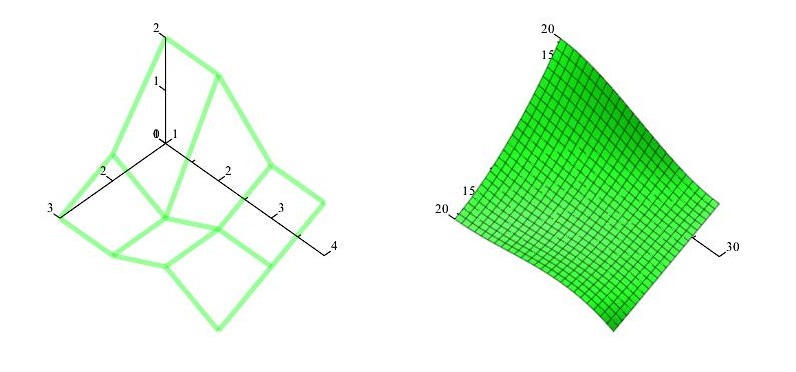
Plát R napojený podél u-okraje, spojitost $C^0$:

\[ \begin{matrix} (0,-30,0)&(0,-20,0)&(0,-10,0)&(0,0,20)&\mid &(0,0,20) & \cdots & (0,30,10) \\ (10,-30,0) & (10,-20,0) & (10,-10,0) & (10,0,5)&\mid&(10,0,5) & ~ & \vdots \\ (20,-30,0) & (20,-20,0) & (20,-10,0) & (20,0,0)&\mid&(20,0,0) & ~\cdots & (20,30,0) \end{matrix}\]
Mapa plátu $R$

\[ M_R= \begin{pmatrix} (0,-30,0)&(0,-20,0)&(0,-10,0)&(0,0,20) \\ (10,-30,0) & (10,-20,0) & (10,-10,0) & (10,0,5) \\ (20,-30,0) & (20,-20,0) & (20,-10,0) & (20,0,0) \end{pmatrix}\]
Plát R napojený podél u-okraje, spojitost $C^0$:
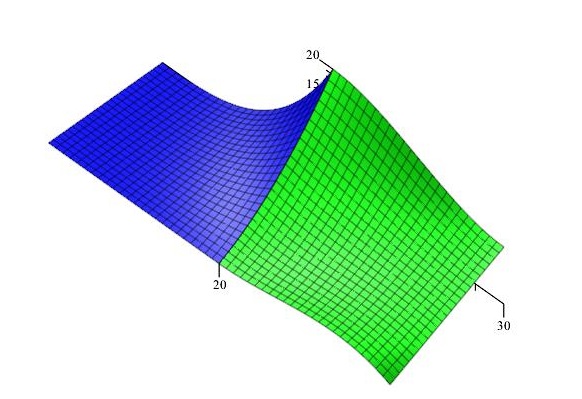
Plát S napojený podél v-okraje, spojitost $C^1$:

\[ \begin{matrix} (0,0,20) & (0,10,20) & (0,20,10) & (0,30,10) \\ (10,0,5) & (10,10,0) & (10,20,5) & (10,30,5) \\ (20,0,0) & (20,10,0) & (20,20,5) & (20,30,0) \\ --- & --- & --- & --- \\ (20,0,0) & (20,10,0) & (20,20,5) & (20,30,0)\\ (30,0,-5)&(30,10,0)&(30,20,5)&(30,30,-5)\\ (40,0,0)&(40,10,0)&(40,20,0)&(40,30,0) \end{matrix}\]
Mapa plátu $S$:

\[ M_S= \begin{pmatrix} (20,0,0) & (20,10,0) & (20,20,5) & (20,30,0)\\ (30,0,-5)&(30,10,0)&(30,20,5)&(30,30,-5)\\ (40,0,0)&(40,10,0)&(40,20,0)&(40,30,0) \end{pmatrix}\]
Plát S napojený podél v-okraje, spojitost $C^1$:
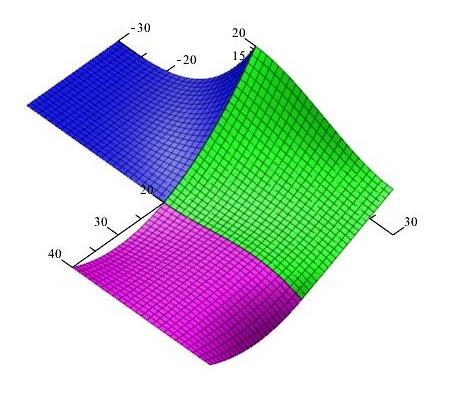
Plát T napojený podél u-okraje, spojitost $C^2$:

\[ \begin{matrix} \cdots & (0,10,20) & (0,20,10) & (0,30,10)&\mid & (0,30,10) & (0,40,10) & (0,50,20) & (0,60,0) \\ \vdots & (10,10,0) & (10,20,5) & (10,30,5)&\mid & (10,30,5) & (10,40,5) & (10,50,0) & (10,60,0)\\ \cdots & (20,10,0) & (20,20,5) & (20,30,0) &\mid & (20,30,0) & (20,40,-5) & (20,50,-20) & (20,60,0) \end{matrix}\]
Mapa plátu $T$

\[ M_T= \begin{pmatrix} (0,30,10) & (0,40,10) & (0,50,20) & (0,60,0) \\ (10,30,5) & (10,40,5) & (10,50,0) & (10,60,0) \\ (20,30,0) & (20,40,-5) & (20,50,-20) & (20,60,0) \end{pmatrix}\]
Plát T napojený podél u-okraje, spojitost $C^2$:

Uniformní Ukotvená Bikubická
B-spline plocha

  • aproximační plocha - segmentovaná
  • dána sítí řídících bodů (minimálně 4x4)
  • okraje jsou ukotvené kubiky
  • jednotlivé segmenty jsou Bézierovy bikubické pláty (řídící body z konstrukce segmentů řádkových a sloupcových ukotvených kubik)
  • všechny segmenty jsou na sebe napojeny s $C^2$ spojitostí
  • zobecněním těchto ploch jsou NeUniformní Racionální B-Spline plochy (NURBS)

Příklad

Je dán Bézierův bikubický plát $P(u,v)$ mapou $M_P$. Určete mapu $M_R$ dalšího Bézierova bikubického plátu $R(s,t)$, který bude napojen na $P(u,v)$ podél křivky $P_1(u)$ se spojitostí $C^2$ (u bodů neovlivňujících spojitost volte z-souřadnici nulovou). Určete také řídicí body (= mapu plátu $M_T$) ukotvené bikubické (B-spline) plochy $T$, která je tvořena segmenty $P$ a $R$.

\[ M_P= \begin{pmatrix} (0,0,3) & (0,1,0) & (0,2,3) & (0,3,1) \\ (1,0,2) & (1,1,1) & (1,2,2) & (1,3,1) \\ (2,0,4) & (2,1,1) & (2,2,1) & (2,3,0) \\ (3,0,0) & (3,1,0) & (3,2,0) & (3,3,0) \end{pmatrix} \]
Podle podmínek $\color{blue}{C^0},\color{green}{C^1}$ a $\color{red}{C^2}$ spojitosti řádkových Bézierových kubik doplnit z-souřadnice plátu $R$

\[M_{P_z}|M_{R_z}=\begin{pmatrix} 3 & 0 & 3 & 1 & | & \color{blue}{1} & \color{green}{-1} & \color{red}{-8} & 0 \\ 2 & 1 & 2 & 1 & | & \color{blue}{1} & \color{green}{0} & \color{red}{-3} & 0 \\ 4 & 1 & 1 & 0 & | & \color{blue}{0} & \color{green}{-1} & \color{red}{-3} & 0 \\ 0 & 0 & 0 & 0 & | & \color{blue}{0} & \color{green}{0} & \color{red}{0} & 0 \\ \end{pmatrix} \]
Mapa plátu $R$

\[ M_R= \begin{pmatrix} (0,3,1) & (0,4,-1) & (0,5,-8) & (0,6,0) \\ (1,3,1) & (1,4,0) & (1,5,-3) & (1,6,0) \\ (2,3,0) & (2,4,-1) & (2,5,-3) & (2,6,0) \\ (3,3,0) & (3,4,0) & (3,5,0) & (3,6,0) \end{pmatrix} \]
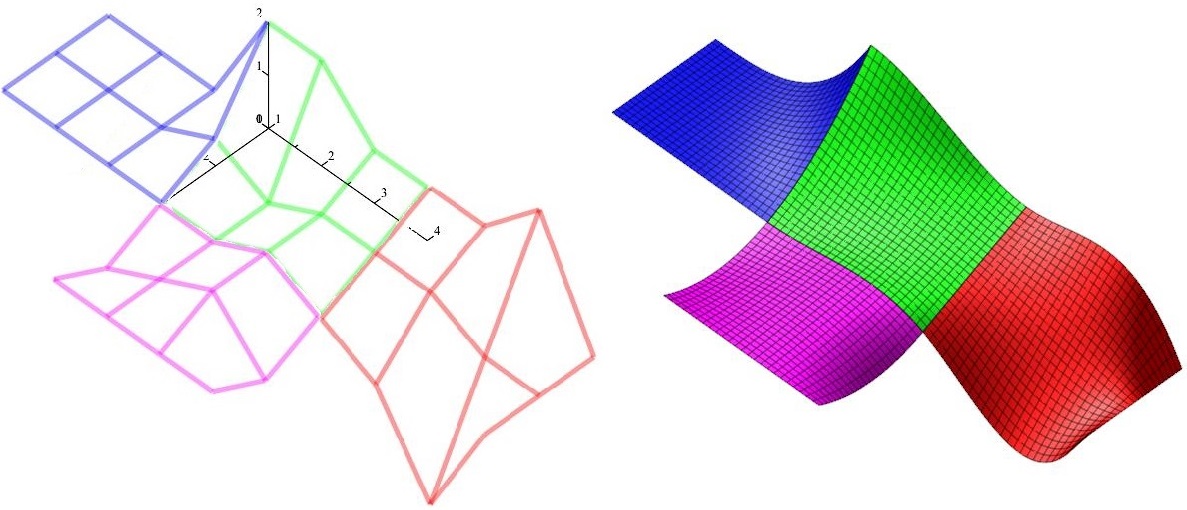
Konstrukce bodů mapy $M_R$

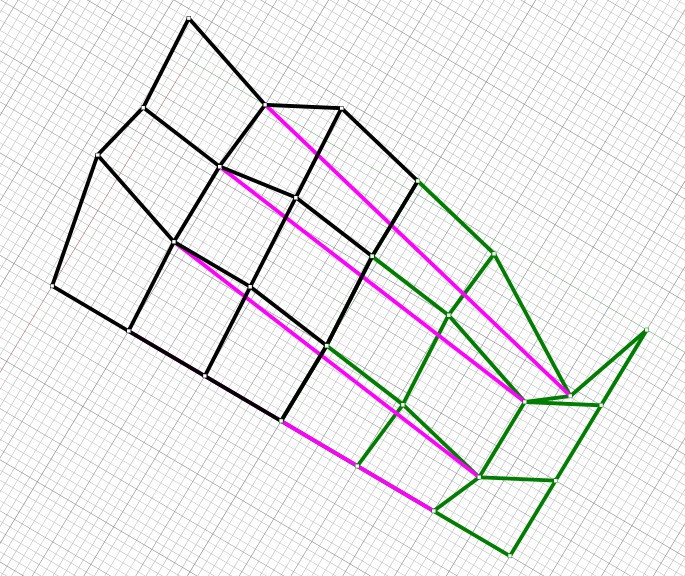
Kontrola napojení plátů $P$ a $R$ zebřími pruhy

Místo společného uzlu každé řádkové ukotvené kubiky doplnit její řídicí bod (= spojit dvě Bézierovy kubiky do jedné ukotvené kubiky) a odstranit z každé kubiky jeden další bod (pro ukotvenou není řídicí, leží v polovině ramene)

\[ \begin{matrix} (0,0,3) & (0,1,0) & \color{blue}{(0,2,3)} & \color{red}{(0,3,1)} & | & \color{red}{(0,3,1)} & \color{blue}{(0,4,-1)} & (0,5,-8) & (0,6,0) \end{matrix} \]
\[\Downarrow\]
\[ \begin{matrix} (0,0,3) & (0,1,0) & \boldsymbol{\color{red}{(0,3,6)}} & (0,5,-8) & (0,6,0) \end{matrix} \]
Konstrukce bodů mapy $M_T$ ukotvené plochy

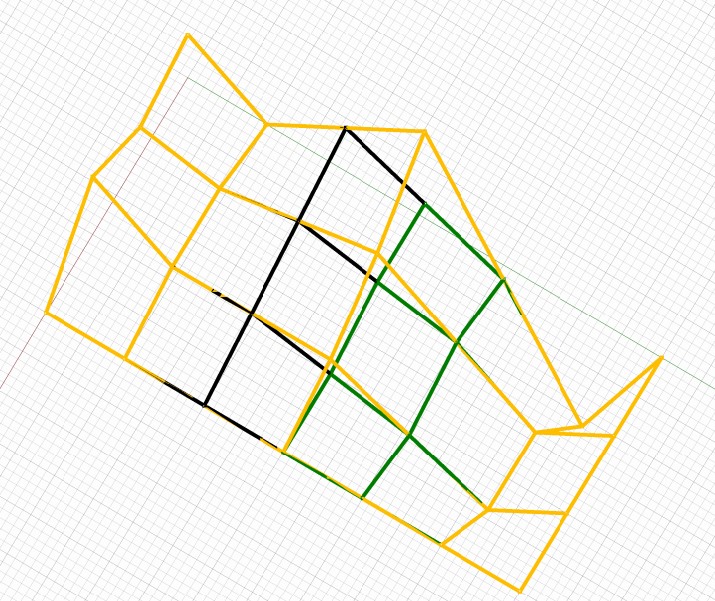
Mapa ukotvené bikubické plochy

\[ M_T= \begin{pmatrix} (0,0,3) & (0,1,0) & \color{red}{(0,3,6)} & (0,5,-8) & (0,6,0) \\ (1,0,2) & (1,1,1) & \color{red}{(1,3,3)} & (1,5,-3) & (1,6,0) \\ (2,0,4) & (2,1,1) & \color{red}{(2,3,1)} & (2,5,-3) & (2,6,0) \\ (3,0,0) & (3,1,0) & \color{red}{(3,3,0)} & (3,5,0) & (3,6,0) \end{pmatrix} \]
Ukotvená plocha $T$

Pláty Bézierových ploch a ukotvená plocha $T$

Příklad

Určete řídicí body jednotlivých plátů Bézierových bikubických ploch, ze kterých je složena ukotvená bikubická B-spline plocha daná mapou M,

\[ M= \begin{pmatrix} (0,0,0) & (0,10,0) & (0,20,0) & (0,30,0) & (0,40,0) \\ (10,0,0) & (10,10,5) & (10,20,5) & (10,30,25) & (10,40,0)\\ (20,0,0) & (20,10,-5) & (20,20,-5) & (20,30,15) & (20,40,0) \\ (30,0,0) & (30,10,25) & (30,20,-15) & (30,30,45) & (30,40,0) \\ (40,0,0) & (40,10,0) & (40,20,0) & (40,30,0) & (40,40,0) \end{pmatrix} \]
Řídicí síť ukotvené plochy

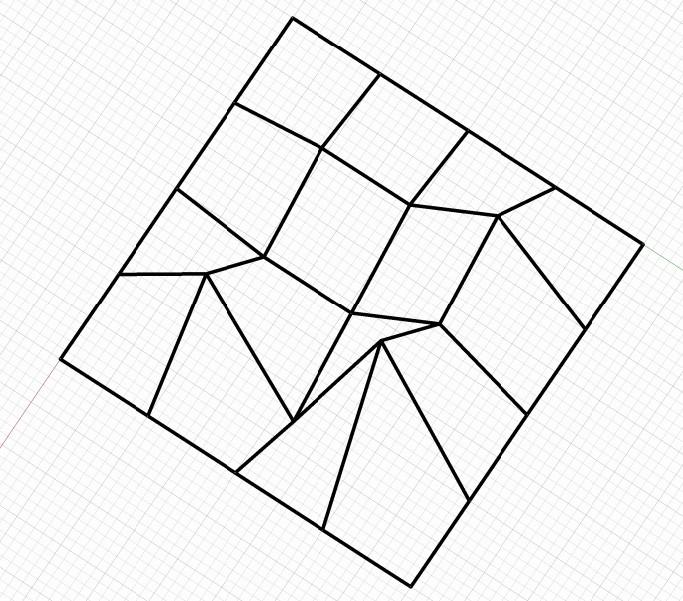
Ukotvená plocha

Po řádcích doplnit řídicí body segmentů (jsou to Bézierovy kubiky) ukotvených kubik
viz. například druhý řádek

\[ \begin{matrix} (10,0,0) & (10,10,5) & (10,20,5) & (10,30,25) & (10,40,0) \end{matrix} \]
\[\Downarrow \]
\[ \begin{matrix} (10,0,0) & (10,10,5) & \color{blue}{(10,15,5)} & \color{red}{(10,20,10)} & \color{blue}{(10,25,15)} & (10,30,25) & (10,40,0) \end{matrix} \]
Konstrukce řídicích bodů "řádkových" segmentů

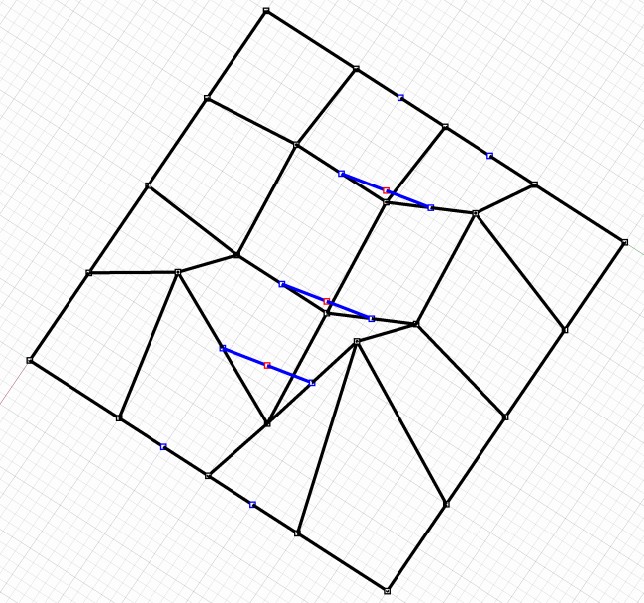
Nová "mapa" plátu je nyní typu 5x7

$\tilde{M}= \begin{pmatrix} (0,0,0) & (0,10,0) & \color{blue}{(0,15,0)} & \color{red}{(0,20,0)} & \color{blue}{(0,25,0)} & (0,30,0) & (0,40,0) \\ (10,0,0) & (10,10,5) & \color{blue}{(10,15,5)} & \color{red}{(10,20,10)} & \color{blue}{(10,25,15)} & (10,30,25) & (10,40,0) \\ (20,0,0) & (20,10,-5) & \color{blue}{(20,15,-5)} & \color{red}{(20,20,0)} & \color{blue}{(20,25,5)} & (20,30,15) & (20,40,0) \\ (30,0,0) & (30,10,25) & \color{blue}{(30,15,5)} & \color{red}{(30,20,10)} & \color{blue}{(30,25,15)} & (30,30,45) & (30,40,0) \\ (40,0,0) & (40,10,0) & \color{blue}{(40,15,0)} & \color{red}{(40,20,0)} & \color{blue}{(40,25,0)} & (40,30,0) & (40,40,0) \end{pmatrix} $
Stejnou konstrukci nyní provést i pro sloupcové ukotvené kubiky $\rightarrow$ matice 7x7
Konstrukce řídicích bodů "sloupcových" segmentů


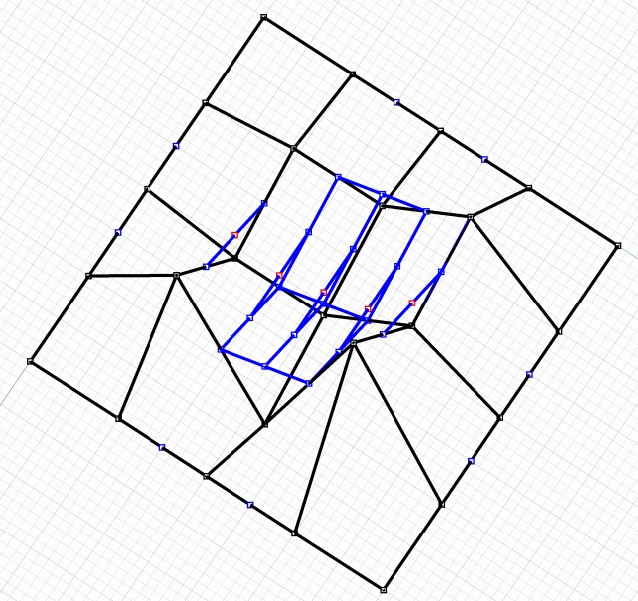
"Rohové" matice 4x4 vybrané z matice $\bar{M}$ jsou mapy plátů jednotlivých Bézierových bikubických ploch, které jsou na sebe napojené s $C^2$ spojitostí a tvoří segmenty původní ukotvené bikubické B-spline plochy.
"Mapa" napojených plátů Bézierových bikubických ploch

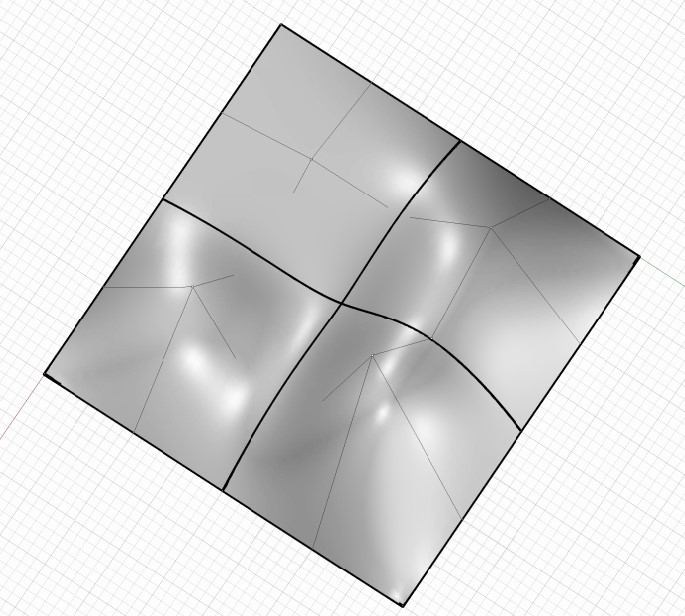
Pláty Bézierových bikubických ploch

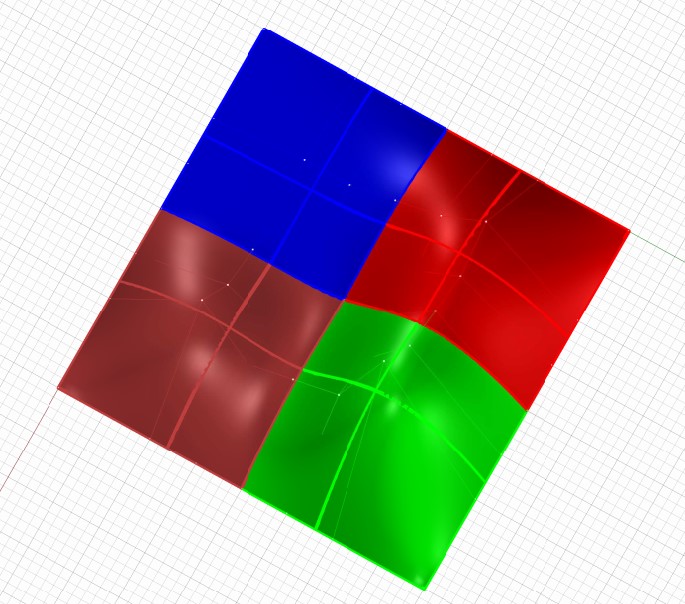
Kontrola spojitosti plátů a srovnání s ukotvenou plochou

Děkuji za pozornost ;)