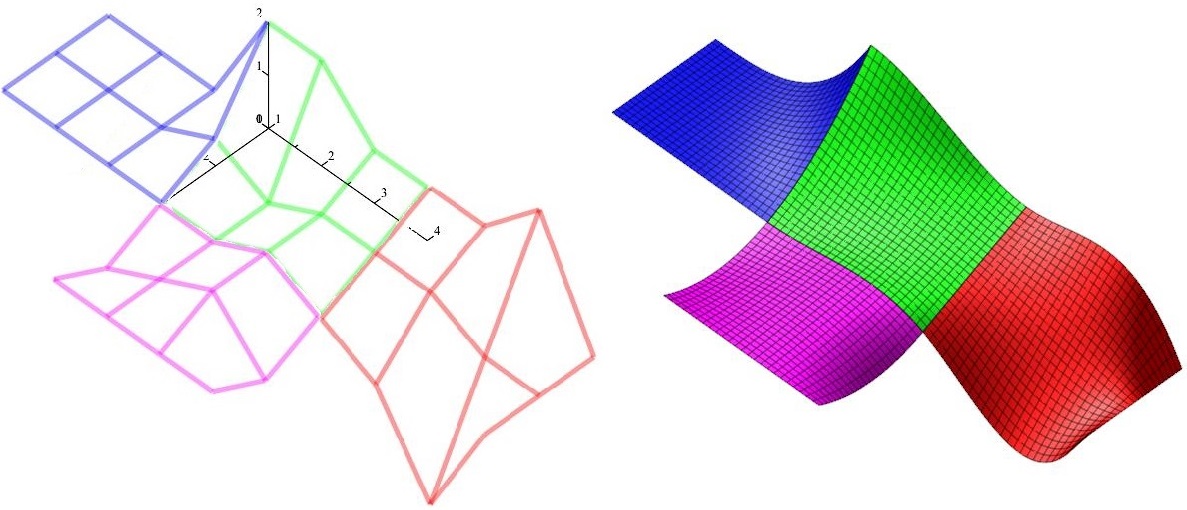
Počítačová grafika 2022/23
Bézierova plocha
Bézierova plocha - vlastnosti
- interpoluje rohy řídící sítě
- okraje plátu jsou Bézierovy křivky
- tečné vektory v rozích plátu jsou násobky krajních ramen řídících polygonů okrajových křivek
- vektor zkrutu v rohu plátu je určen řídícími body rohového oka sítě
- jestliže je rohové oko sítě rovnoběžník, je vektor zkrutu nulový
Vztahy mezi plochami
Coonsova bilineární $\to$ Bézierova
Coonsova bilineární plocha
mapa plátu
\[ M = \begin{pmatrix} -P_{0,0} & P_{0}(v) & -P_{0,1} \\ P_{0}(u) & \vec{0} & P_{1}(u) \\ -P_{1,0} & P_{1}(v) & -P_{1,1} \\ \end{pmatrix} \]
Coonsova bilineární plocha
speciálně: okrajové křivky - Bézierovy kubiky
\[ \begin{matrix} ~ & ~ & ~ & ~ & P_{0}(v) & ~ & ~ & ~ & ~ \\ ~ & V_{0,0} & \to & V_{0,1} & \to & V_{0,2} & \to & V_{0,3} & ~ \\ ~ & \downarrow & ~ & ~ & ~ & ~ & ~ & \downarrow & \\ ~ & V_{1,0} & ~ & ~ & ~ & ~ & ~ & V_{1,3} & \\ P_{0}(u) & \downarrow & ~ & ~ & ~ & ~ & ~ & \downarrow & P_{1}(u)\\ ~ & V_{2,0} & ~ & ~ & ~ & ~ & ~ & V_{2,3} & \\ ~ & \downarrow & ~ & ~ & ~ & ~ & ~ & \downarrow & \\ ~ & V_{3,0} & \to & V_{3,1} & \to & V_{3,2} & \to & V_{3,3} & ~ \\ ~ & ~ & ~ & ~ & P_{1}(v) & ~ & ~ & ~ & ~ \\ \end{matrix} \]
Coonsova bilineární plocha
okrajové křivky - Bézierovy kubiky
\[ M = \begin{pmatrix} -V_{0,0} & P_{0}(v) & -V_{0,3} \\ P_{0}(u) & \vec{0} & P_{1}(u) \\ -V_{3,0} & P_{1}(v) & -V_{3,3} \\ \end{pmatrix} \]
Coonsova bilineární plocha
$\downarrow $
Bézierova bikubická plocha
?
Bézierova plocha
mapa plátu
\[ M = \begin{pmatrix} V_{0,0} & V_{0,1} & V_{0,2} & V_{0,3} \\ V_{1,0} & ? & ? & V_{1,3} \\ V_{2,0} & ? & ? & V_{2,3} \\ V_{3,0} & V_{3,1} & V_{3,2} & V_{3,3} \end{pmatrix} \]
Coonsova bilineární $\to$ Bézierova
Postup - teorie:
- vektory zkrutu Coonsovy bilineární plochy získat výpočtem (konkrétní vektor v každém rohu)
- vyjádřit vektory zkrutu v rozích Bézierovy plochy (obecně, ve vyjádřeních figurují vnitřní body sítě)
- porovnat dva zkruty (Coons = Bézier) v každém rohu
- z rovnic vyjádřit neznámé vnitřní body sítě
Coonsova bilineární $\to$ Bézierova bikubická
Postup - praxe:
- vektory zkrutu Coonsovy bilineární plochy (rohy): \[P^{uv}(0,0), P^{uv}(0,1), P^{uv}(1,0), P^{uv}(1,1)\]
- vektory zkrutu Bézierovy plochy (obecně) \[ P^{uv}(u,v)=\mathscr{B}^{\prime}(u)\cdot M \cdot \mathscr{B}^{\prime}(v) \] kde \[\mathscr{B}^{\prime}(u) = (B_{03}^{\prime}(u),B_{13}^{\prime}(u),B_{23}^{\prime}(u),B_{33}^{\prime}(u))\] \[\mathscr{B}^{\prime}(v) = (B_{03}^{\prime}(v),B_{13}^{\prime}(v),B_{23}^{\prime}(v),B_{33}^{\prime}(v))^T\]
- konkrétně v rozích \[ \mathscr{B}^{\prime}(0)=(-3,3,0,0), \mathscr{B}^{\prime}(1)=(0,0,-3,3)\]
Coonsova bilineární $\to$ Bézierova bikubická
Roh $P_{0,0}$
- vektor zkrutu Bézierovy plochy: \[ P^{uv}(0,0)=(-3,3,0,0)\cdot M \cdot (-3,3,0,0)^T \] \[\Downarrow\] \[P^{uv}(0,0)=9V_{0,0}-9V_{1,0}-9V_{0,1}+9V_{1,1}\] \[\Downarrow\] \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) - V_{0,0}+V_{1,0}+V_{0,1} \] \[\Downarrow\] \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) - V_{0,0}+V_{1,0}+V_{0,1} + (V_{0,0}-V_{0,0})\] \[\Downarrow\] \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) + V_{0,0} + \vec{V_{0,0}V_{1,0}} + \vec{V_{0,0}V_{0,1}} \]
Coonsova bilineární $\to$ Bézierova bikubická
Roh $P_{0,0}$
- pomocí vektoru zkrutu a tečných vektorů Coonsovy bilineární plochy: \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) + V_{0,0} + \vec{V_{0,0}V_{1,0}} + \vec{V_{0,0}V_{0,1}} \] \[\Downarrow\] \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) + V_{0,0} + \frac{1}{3}P^{u}(0,0) + \frac{1}{3}P^{v}(0,0)\]
Coonsova bilineární $\to$ Bézierova bikubická
Roh $P_{1,0}$
- vektor zkrutu Bézierovy plochy: \[ P^{uv}(1,0)=(0,0,-3,3)\cdot M \cdot (-3,3,0,0)^T \] \[\Downarrow\] \[P^{uv}(1,0)=9V_{2,0}-9V_{3,0}-9V_{2,1}+9V_{3,1}\] \[\Downarrow\] \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) - V_{3,0}+V_{2,0}+V_{3,1} \] \[\Downarrow\] \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) - V_{3,0}+V_{2,0}+V_{3,1} + (V_{3,0}-V_{3,0})\] \[\Downarrow\] \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) + V_{3,0} + \vec{V_{3,0}V_{2,0}} + \vec{V_{3,0}V_{3,1}} \]
Coonsova bilineární $\to$ Bézierova bikubická
Roh $P_{1,0}$
- pomocí vektoru zkrutu a tečných vektorů Coonsovy bilineární plochy: \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) + V_{3,0} + \vec{V_{3,0}V_{2,0}} + \vec{V_{3,0}V_{3,1}} \] \[\Downarrow\] \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) + V_{3,0} - \frac{1}{3}P^{u}(1,0) + \frac{1}{3}P^{v}(1,0)\]
Coonsova bilineární $\to$ Bézierova bikubická
Podobně ve zbylých rozích:
\[V_{1,1}= V_{0,0} + \frac{1}{3}P^{u}(0,0) + \frac{1}{3}P^{v}(0,0) + \frac{1}{9}P^{uv}(0,0)\]
\[V_{2,1}= V_{3,0} - \frac{1}{3}P^{u}(1,0) + \frac{1}{3}P^{v}(1,0) - \frac{1}{9}P^{uv}(1,0)\]
\[V_{1,2}= V_{0,3} + \frac{1}{3}P^{u}(0,1) - \frac{1}{3}P^{v}(0,1) - \frac{1}{9}P^{uv}(0,1)\]
\[V_{2,2}= V_{3,3} - \frac{1}{3}P^{u}(1,1) - \frac{1}{3}P^{v}(1,1) + \frac{1}{9}P^{uv}(1,1)\]
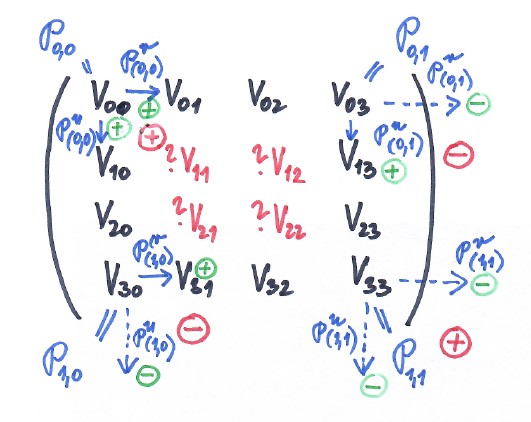
Coonsova bilineární $\to$ Bézierova bikubická
Pomocné schema pro určení znamének:
Příklad
Coonsova bilineární plocha $P_C(u,v)$ je dána řídicími polygony okrajových Bézierových kubik
\[P_0(u): V_{0,0}=(0,0,2), V_{1,0}=(1,0,2), V_{2,0}=(2,0,1), V_{3,0}=(3,0,0) \]
\[P_1(u): V_{0,3}=(0,3,2), V_{1,3}=(1,3,1), V_{2,3}=(2,3,0), V_{3,3}=(3,3,0) \]
\[P_0(v): V_{0,0}=(0,0,2), V_{0,1}=(0,1,1), V_{0,2}=(0,2,1), V_{0,3}=(0,3,2) \]
\[P_1(v): V_{3,0}=(3,0,0), V_{3,1}=(3,1,0), V_{3,2}=(3,2,0), V_{3,3}=(3,3,0) \] Předpokládejte, že Coonsova bilineární plocha $P_C(u,v)$ je plát Bézierovy bikubické plochy $P_B(u,v)$ určený mapou $M$. Určete souřadnice vnitřních bodů mapy $M$.
Příklad
Rovnice okrajových (Bézierových) křivek
\[P_0(u)=(3u,0,u^3-3u^2+2)\] \[P_1(u)=(3u,3,u^3-3u+2)\] \[P_0(v)=(0,3v,3v^2-3v+2)\] \[P_1(v)=(3,3v,0)\phantom{eeeeeeeee}\]
\[ u\in[0,1], v\in[0,1]\]
Příklad
Mapa $M_C$ plátu Coonsovy bilineární plochy
\[ M_C = \begin{pmatrix} -(0,0,2) & (0,3v,3v^2-3v+2) & -(0,3,2) \\ (3u,0,u^3-3u^2+2) & \vec{0} & (3u,3,u^3-3u+2) \\ -(3,0,0) & (3,3v,0) & -(3,3,0) \\ \end{pmatrix} \]
Příklad
Vektorová rovnice Coonsovy bilineární plochy $P_C(u,v)$
\[P_C(u,v)=(1-u,1,u)\cdot M_C \cdot (1-v,1,v)^T\] \[\Downarrow\] \[P_C(u,v)=(3u,3v,3u^3v-3uv^3-u^3-6u^2v+6uv^2+2v^3+3u^2-3v^2-3u+2) \]
Příklad
Rovnice tečných vektorů
\[P^u(u,v)=(3,0,9u^2v-3v^3-3u^2-12uv+6v^2+6u-3)\] \[P^v(u,v)=(0,3,3u^3-9uv^2-6u^2+12uv+6v^2-6v) \]
a rovnice vektorů zkrutu
\[P^{uv}(u,v)=(0,0,9u^2-9v^2-12u+12v)\]
Příklad
Vektory zkrutu v rozích
\[P^{uv}(0,0)=(0,0,0)\] \[P^{uv}(1,0)=(0,0,-3)\] \[P^{uv}(0,1)=(0,0,3)\] \[P^{uv}(1,1)=(0,0,0)\]
+ spočítat tečné vektory v obou směrech (v rozích)
Příklad
Použít vzorce
\[V_{1,1}= V_{0,0} + \frac{1}{3}P^{u}(0,0) + \frac{1}{3}P^{v}(0,0) + \frac{1}{9}P^{uv}(0,0)\] \[V_{2,1}= V_{3,0} - \frac{1}{3}P^{u}(1,0) + \frac{1}{3}P^{v}(1,0) - \frac{1}{9}P^{uv}(1,0)\] \[V_{1,2}= V_{0,3} + \frac{1}{3}P^{u}(0,1) - \frac{1}{3}P^{v}(0,1) - \frac{1}{9}P^{uv}(0,1)\] \[V_{2,2}= V_{3,3} - \frac{1}{3}P^{u}(1,1) - \frac{1}{3}P^{v}(1,1) + \frac{1}{9}P^{uv}(1,1)\]
a dopočítat souřadnice hledaných bodů :)
Příklad
Správný výsledek
\[V_{1,1}= (1,1,1)\\ V_{2,1}= (2,1,\frac{1}{3})\\ V_{1,2}= (1,2,\frac{2}{3}) \\ V_{2,2}= (2,2,0)\]
Příklad
Mapa $M$ plátu Bézierovy plochy
\[ M = \begin{pmatrix} (0,0,2) & (0,1,1) & (0,2,1) & (0,3,2) \\ (1,0,2) & (1,1,1) & (1,2,\frac{2}{3} ) & (1,3,1) \\ (2,0,1) & (2,1,\frac{1}{3}) & (2,2,0) & (2,3,0) \\ (3,0,0) & (3,1,0) & (3,2,0) & (3,3,0) \end{pmatrix} \]
Coonsova bilineární $\to$ Bézierova
kvadraticko-kubická (*)
Coonsova bilineární plocha daná okrajovými Bézierovými křivkami
$\Downarrow$
Coonsova bilineární plocha jako Bézierova plocha?
$\Downarrow$
$\Downarrow$
Coonsova bilineární plocha jako Bézierova plocha?
$\Downarrow$
Coonsova bilineární $\to$ Bézierova
kvadraticko-kubická (*)
vektory zkrutu v rozích plátu totožné
$\Downarrow$
vektory zkrutu z rovnice Coonsovy bilineární plochy
$\Downarrow$
$\Downarrow$
vektory zkrutu z rovnice Coonsovy bilineární plochy
$\Downarrow$
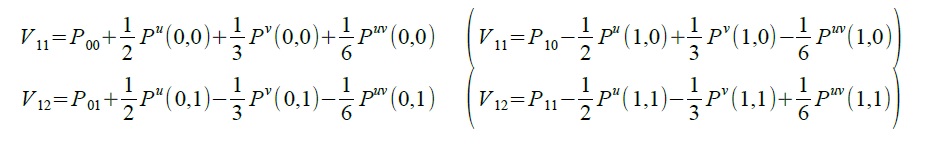
Příklad (*)
vektorová rovnice Coonsovy bilineární plochy:
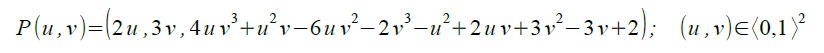
mapa Bézierova plátu:
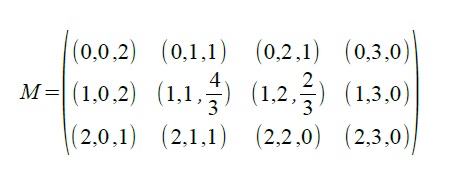
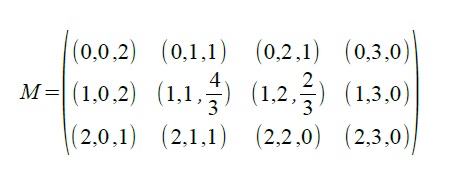
Plátování
Plátování
Uvažujme dva pláty $P(u,v);(u,v)\in[0,1]^2$ a $R(\bar{u},\bar{v});(\bar{u},\bar{v})\in[0,1]^2$.
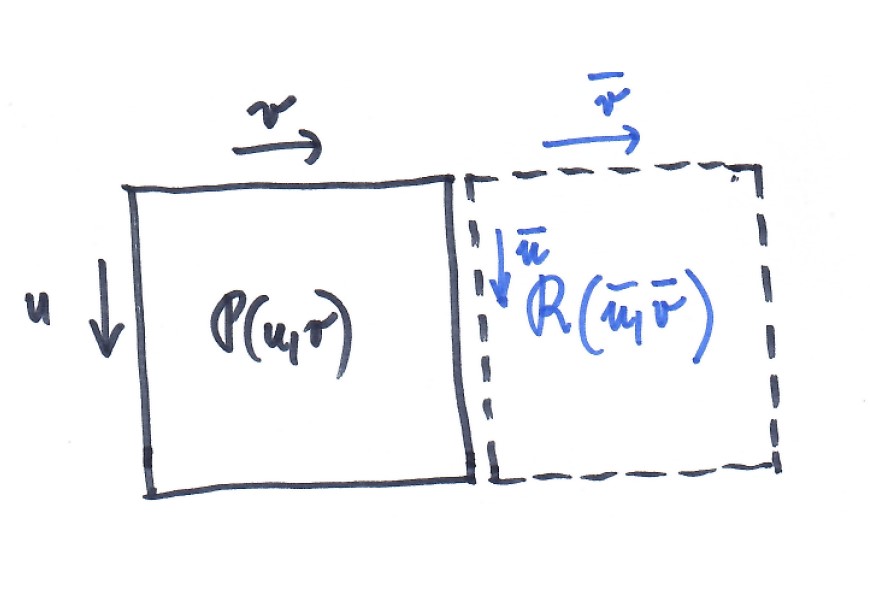
Plátování
spojitost plátů je definována pomocí spojitosti napojení podél okrajové křivky
$C^0$ spojitost $\Leftrightarrow$ společná okrajová křivka
$C^1$ spojitost $\Leftrightarrow$ $C^0$ + stejné příčné tečné vektory v bodech společné okrajové křivky
$C^2$ spojitost $\Leftrightarrow$ $C^1$ + stejné příčné vektory druhých derivací v bodech společné okrajové křivky
Plátování interpolačních ploch
přímková přechodová plocha (hyper. paraboloid) - ve směru úseček pouze $C^0$ spojitost
Coonsova bilineární plocha - podél křivky napojení lze zaručit pouze $C^0$ spojitost
Plátování Bézierových ploch
tady řešeno pouze napojení plátů stejného typu!
\[ M_P= \begin{pmatrix} V_{0,0} & \cdots & V_{0,n} \\ \vdots & ~ & \vdots \\ V_{m,0} & \cdots & V_{m,n} \end{pmatrix}, M_R= \begin{pmatrix} U_{0,0} & \cdots & U_{0,n} \\ \vdots & ~ & \vdots \\ U_{m,0} & \cdots & U_{m,n} \end{pmatrix} \]
Plátování Bézierových ploch
$C^n$ spojité napojení $(n=0,1,2)$ podél u-okraje
$\Downarrow \Uparrow$
stejný sloupec + po řádcích splněny podmínky $C^n$ spojitosti Bezierových v-křivek
$\Downarrow \Uparrow$
stejný sloupec + po řádcích splněny podmínky $C^n$ spojitosti Bezierových v-křivek
$C^n$ spojité napojení $(n=0,1,2)$ podél v-okraje
$\Downarrow \Uparrow$
stejný řádek + po sloupcích splněny podmínky $C^n$ spojitosti Bezierových u-křivek
$\Downarrow \Uparrow$
stejný řádek + po sloupcích splněny podmínky $C^n$ spojitosti Bezierových u-křivek
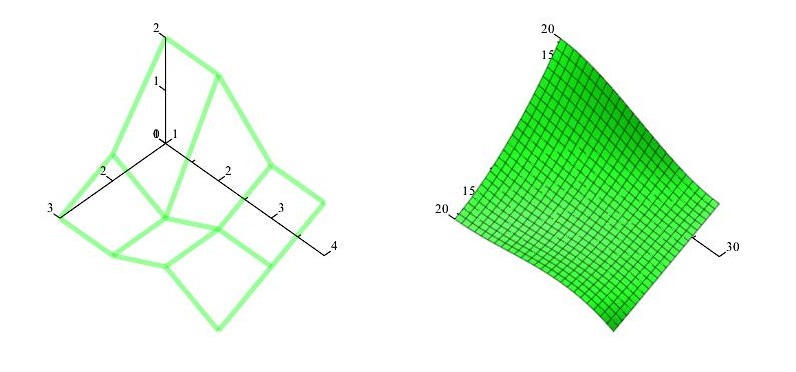
Příklad
Bézierova plocha $P$ je dána mapou
\[ M_P = \begin{pmatrix}
(0,0,20) & (0,10,20) & (0,20,10) & (0,30,10) \\
(10,0,5) & (10,10,0) & (10,20,5) & (10,30,5) \\
(20,0,0) & (20,10,0) & (20,20,5) & (20,30,0)
\end{pmatrix}
\]Určete mapu $M_R$ Bézierovy plochy $R$, která je napojena k ploše $P$ podél okraje $P_0(u)$ se spojitostí $C^0$.
Určete mapu $M_S$ Bézierovy plochy $S$, která je napojena k ploše $P$ podél okraje $P_1(v)$ se spojitostí $C^1$.
Určete mapu $M_T$ Bézierovy plochy $T$, která je napojena k ploše $P$ podél okraje $P_1(u)$ se spojitostí $C^2$.
Všechny plochy jsou stejného typu, z-ové souřadnice bodů, které neovlivní danou spojitost volte nulové.
Určete mapu $M_S$ Bézierovy plochy $S$, která je napojena k ploše $P$ podél okraje $P_1(v)$ se spojitostí $C^1$.
Určete mapu $M_T$ Bézierovy plochy $T$, která je napojena k ploše $P$ podél okraje $P_1(u)$ se spojitostí $C^2$.
Všechny plochy jsou stejného typu, z-ové souřadnice bodů, které neovlivní danou spojitost volte nulové.
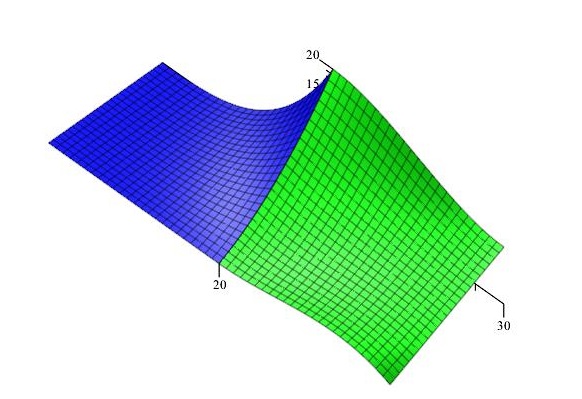
Plát R napojený podél $P_0(u)$ okraje, spojitost $C^0$:
\[ \begin{matrix} (0,-30,0)&(0,-20,0)&(0,-10,0)&(0,0,20)&\mid &(0,0,20) & \cdots & (0,30,10) \\ (10,-30,0) & (10,-20,0) & (10,-10,0) & (10,0,5)&\mid&(10,0,5) & ~ & \vdots \\ (20,-30,0) & (20,-20,0) & (20,-10,0) & (20,0,0)&\mid&(20,0,0) & ~\cdots & (20,30,0) \end{matrix}\]
Mapa plátu $R$
\[ M_R= \begin{pmatrix} (0,-30,0)&(0,-20,0)&(0,-10,0)&(0,0,20) \\ (10,-30,0) & (10,-20,0) & (10,-10,0) & (10,0,5) \\ (20,-30,0) & (20,-20,0) & (20,-10,0) & (20,0,0) \end{pmatrix}\]
Plát R napojený podél $P_0(u)$ okraje, spojitost $C^0$:
Plát S napojený podél $P_1(v)$ okraje, spojitost $C^1$:
\[ \begin{matrix} (0,0,20) & (0,10,20) & (0,20,10) & (0,30,10) \\ (10,0,5) & (10,10,0) & (10,20,5) & (10,30,5) \\ (20,0,0) & (20,10,0) & (20,20,5) & (20,30,0) \\ --- & --- & --- & --- \\ (20,0,0) & (20,10,0) & (20,20,5) & (20,30,0)\\ (30,0,-5)&(30,10,0)&(30,20,5)&(30,30,-5)\\ (40,0,0)&(40,10,0)&(40,20,0)&(40,30,0) \end{matrix}\]
Mapa plátu $S$:
\[ M_S= \begin{pmatrix} (20,0,0) & (20,10,0) & (20,20,5) & (20,30,0)\\ (30,0,-5)&(30,10,0)&(30,20,5)&(30,30,-5)\\ (40,0,0)&(40,10,0)&(40,20,0)&(40,30,0) \end{pmatrix}\]
Plát S napojený podél $P_1(v)$ okraje, spojitost $C^1$:
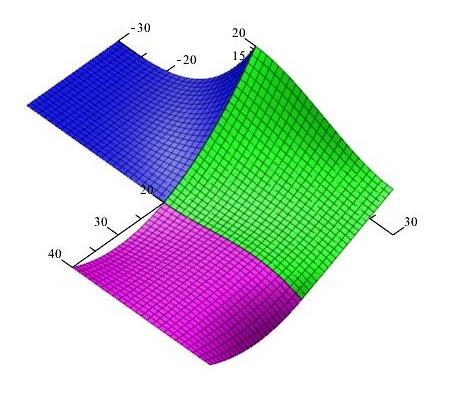
Plát T napojený podél $P_1(u)$ okraje, spojitost $C^2$:
\[ \begin{matrix} \cdots & (0,10,20) & (0,20,10) & (0,30,10)&\mid & (0,30,10) & (0,40,10) & (0,50,20) & (0,60,0) \\ \vdots & (10,10,0) & (10,20,5) & (10,30,5)&\mid & (10,30,5) & (10,40,5) & (10,50,0) & (10,60,0)\\ \cdots & (20,10,0) & (20,20,5) & (20,30,0) &\mid & (20,30,0) & (20,40,-5) & (20,50,-20) & (20,60,0) \end{matrix}\]
Mapa plátu $T$
\[ M_T= \begin{pmatrix} (0,30,10) & (0,40,10) & (0,50,20) & (0,60,0) \\ (10,30,5) & (10,40,5) & (10,50,0) & (10,60,0) \\ (20,30,0) & (20,40,-5) & (20,50,-20) & (20,60,0) \end{pmatrix}\]
Plát T napojený podél $P_1(u)$ okraje, spojitost $C^2$: