Počítačová grafika 2022/23

Plochy

Plocha

každá souvislá podmnožina $\mathbb{E}_3$, která je spojitým obrazem souvislé oblasti $I\subset \mathbb{E}_2$.

  • vektorová rovnice plochy
    $$P(u,v)=(x(u,v),y(u,v),z(u,v)),\ (u,v)\in I$$
  • plát $\iff I=[a,b]\times[c,d]$
  • plát s uniformní parametrizací $\iff I=[0,1]^2$

Plát

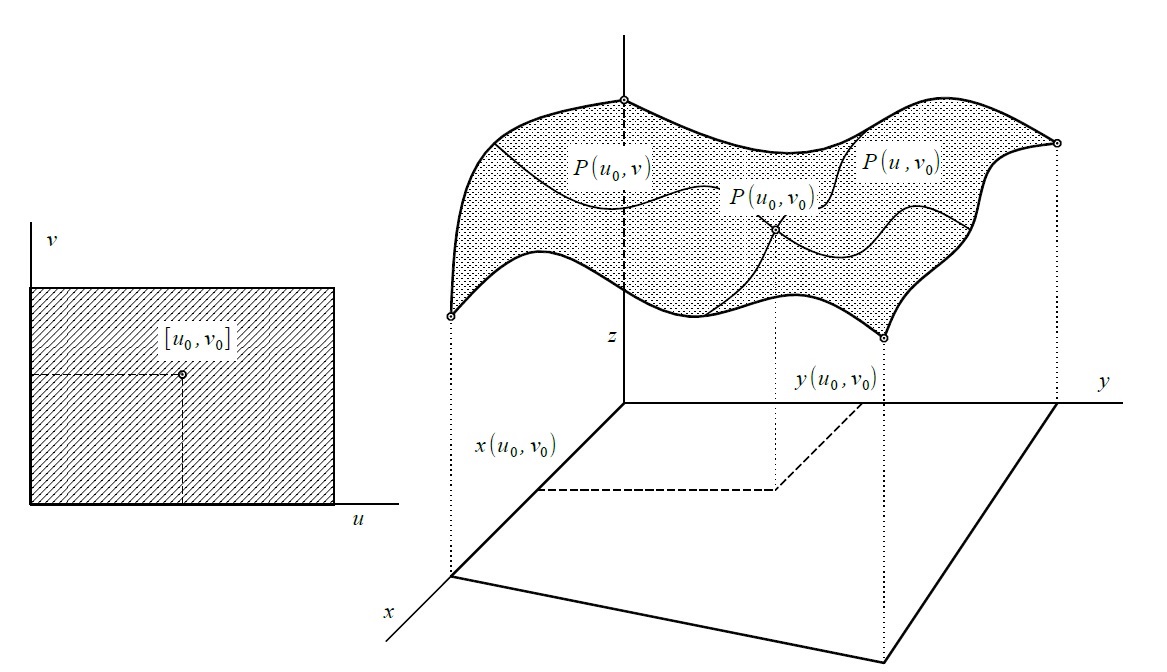
  • parametrické (křivočaré) souřadnice $(u_0,v_0)$ bodu plochy $P(u_0,v_0)$
  • parametrická u-křivka plochy $P(u,v_0)=(x(u,v_0),y(u,v_0),z(u,v_0))=P_{v_0}(u), u\in[a,b]$
  • parametrická v-křivka plochy $P(u_0,v)=P_{u_0}(v), v\in [c,d]$

Plát s uniformní parametrizací

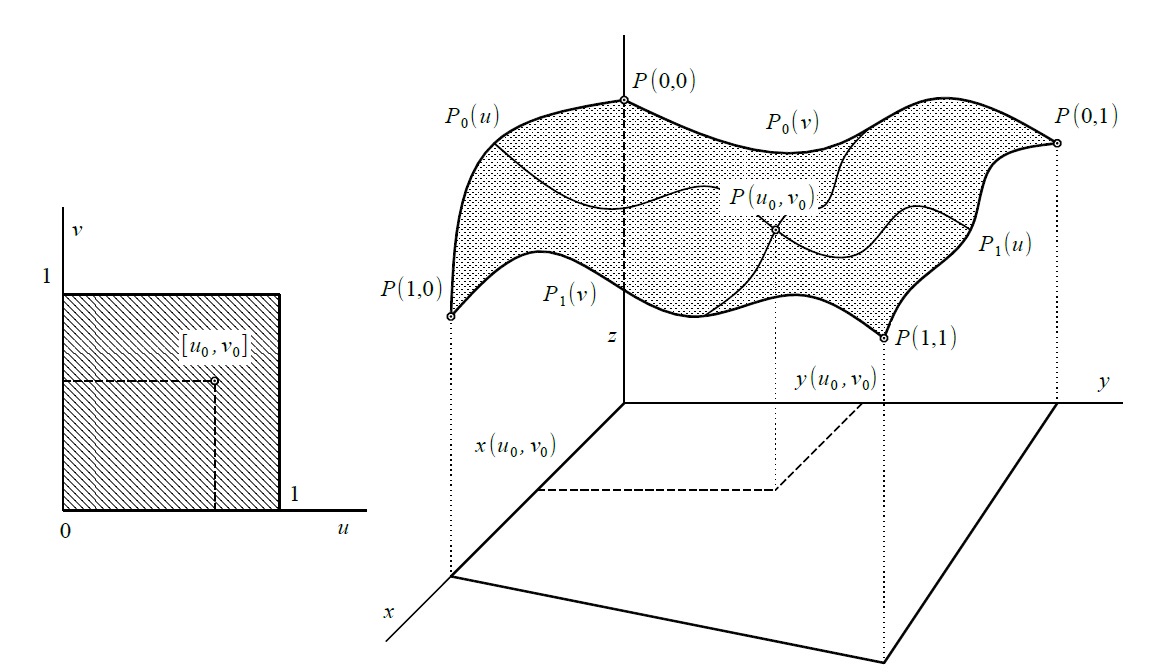
  • rohy plátu $P_{0,0}=P(0,0),P_{0,1}=P(0,1),P_{1,0}=P(1,0),P_{1,1}=P(1,1)$
  • okrajové křivky plátu $P_0(u),P_1(u),P_0(v),P_1(v)$

Plocha

tečné vektory \[P^u(u,v)= \frac{\partial P(u,v)}{\partial u}=\bigg(\frac{\partial x(u,v)}{\partial u},\frac{\partial y(u,v)}{\partial u},\frac{\partial z(u,v)}{\partial u}\bigg)\] \[P^v(u,v)= \frac{\partial P(u,v)}{\partial v}=\bigg(\frac{\partial x(u,v)}{\partial v},\frac{\partial y(u,v)}{\partial v},\frac{\partial z(u,v)}{\partial v}\bigg)\]

tečná rovina a normála

\[\vec{n}(u,v)=P^u(u,v)\times P^v(u,v)\]

vektor zkrutu \[P^{uv}(u,v)=\frac{\partial^2 P(u,v)}{\partial u\partial v}=\frac{\partial^2 P(u,v)}{\partial v\partial u}\]

Přímková přechodová plocha

interpolační plocha mezi dvěma zadanými okraji

Přímková přechodová plocha

Dáno: dva okraje plátu ve směru u (tj. $P_0(u), P_1(u)$)
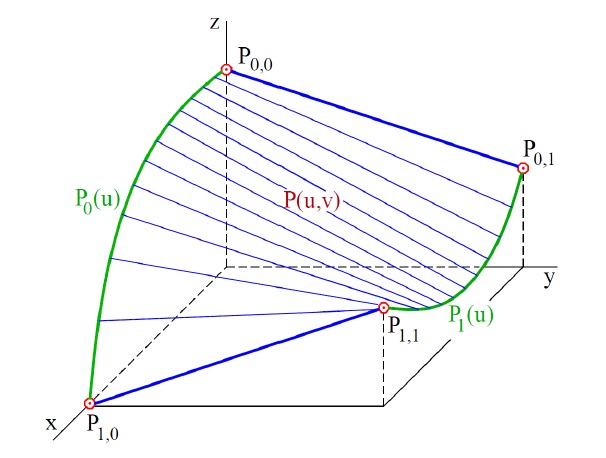
vektorová rovnice: $P(u,v)=(1-v)P_0(u)+vP_1(u), (u,v)\in [0,1]^2$

Přímková přechodová plocha

Dáno: dva okraje ve směru v (tj. $P_0(v), P_1(v)$)
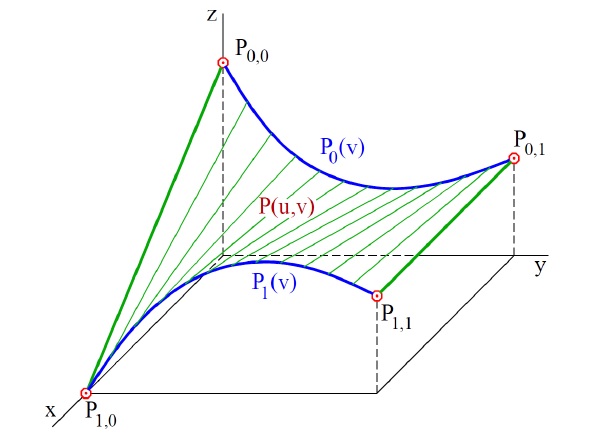
vektorová rovnice: $P(u,v)=(1-u)P_0(v)+uP_1(v), (u,v)\in [0,1]^2$

Přímková přechodová plocha - vlastnosti

  • interpoluje dané okraje
  • parametrické křivky druhého systému než dané okraje jsou úsečky

Příklad

Přímková přechodová plocha je dána okraji
\[P_0(v)=(0,v,1-v^2), P_1(v)=(3,2v,0), v\in[0,1].\]
Určete:
  • vektorovou rovnici plátu
  • vektorové rovnice zbývajících okrajů
  • rohové body plátu
  • tečné vektory v rozích plátu
  • vektory zkrutu v rozích plátu

Plát načrtněte pomocí okrajových křivek.
okraje: $P_0(v)=(0,v,1-v^2), P_1(v)=(3,2v,0)$
vektorová rovnice - obecně: $P(u,v)= (1-u)P_0(v)+uP_1(v), (u,v)\in[0,1]^2$

vektorová rovnice - dosazení:

$P(u,v)=(3u,v(1+u),(1-v^2)(1-u)), (u,v)\in[0,1]^2$

rovnice zbývajích okrajů:

$P_0(u)=(3u,0,1-u),\ P_1(u)=(3u,1+u,0), u\in[0,1]$

rovnice tečných vektorů:

$P^u(u,v)=(3,v,v^2-1)$
$P^v(u,v)=(0,1+u,2v(u-1))$

rovnice vektorů zkrutu:

$P^{uv}(u,v)=(0,1,2v)$
rohové body plátu:

$P_{0,0}=(0,0,1),P_{0,1}=(0,1,0), P_{1,0}=(3,0,0), P_{1,1}=(3,2,0)$

tečné vektory v rozích:

$P^u(0,0)=(3,0,-1),\ P^v(0,0)=(0,1,0)$
$P^u(0,1)=(3,1,0), \ P^v(0,1)=(0,1,-2)$
$P^u(1,0)=(3,0,-1), \ P^v(1,0)=(0,2,0)$
$P^u(1,1)=(3,1,0), \ P^v(1,1)=(0,2,0)$

vektory zkrutu v rozích:

$P^{uv}(0,0)=(0,1,0)$
$P^{uv}(0,1)=(0,1,2)$
$P^{uv}(1,0)=(0,1,0)$
$P^{uv}(1,1)=(0,1,2)$

Přímková přechodová plocha

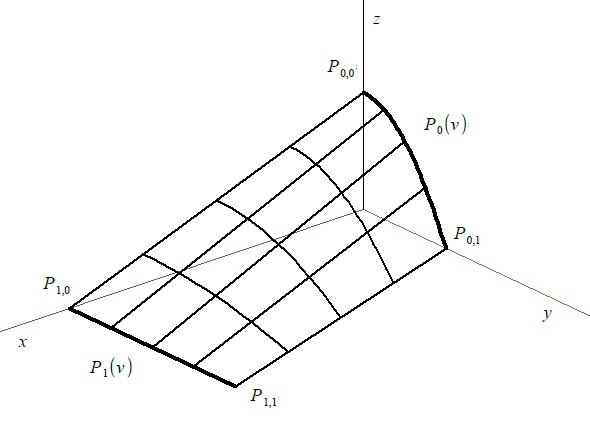
Plocha hyperbolického paraboloidu

interpolační plocha mezi 4 danými body

Plocha hyperbolického paraboloidu

Dáno: rohy plátu (tj. body $P_{0,0}, P_{0,1}, P_{1,0}, P_{1,1}$)

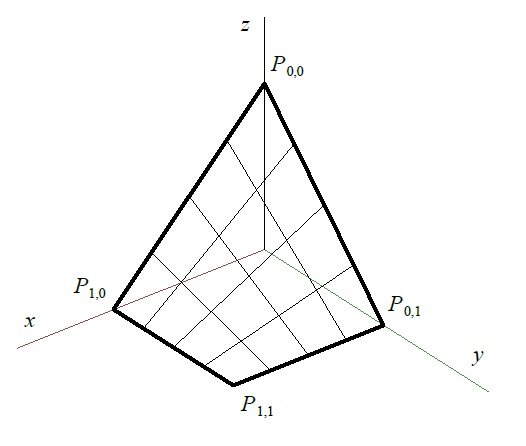
Vektorová rovnice

přímková přechodová plocha mezi dvěma okraji - úsečkami:

úsečka mezi $P_{0,0}$ a $P_{1,0}:$ $P_0(u)=(1-u)P_{0,0}+uP_{1,0}$
úsečka mezi $P_{0,1}$ a $P_{1,1}$: $P_1(u)=(1-u)P_{0,1}+uP_{1,1}$
rovnice přímkové přechodové plochy: $P(u,v)=(1-v)P_0(u)+vP_1(u)$


\[P(u,v)=(1-u)(1-v)P_{0,0}+v(1-u)P_{0,1}+u(1-v)P_{1,0}+uvP_{1,1},\]$(u,v)\in [0,1]^2$

Hyperbolický paraboloid - vlastnosti

  • interpoluje rohy plátu (i okrajové úsečky)
  • parametrické křivky obou soustav jsou úsečky
  • je speciálním případem přímkové přechodové plochy
  • vektor zkrutu je konstantní podél celého plátu

Příště: Cooonsova bilineární plocha
Bézierova plocha