Počítačová grafika 22/23
Coonsova kubika
Coonsův kubický B-spline
Ukotvená B-spline křivka 3. stupně
Coonsův kubický B-spline
Ukotvená B-spline křivka 3. stupně
Coonsova kubika
Steven Anson Coons (1912 - 1979)
Massachusetts Institute of Technology (MIT)
Coonsova kubika
aproximační křivka 3. stupně daná 4 řídícími body $P_0, P_1, P_2, P_3$
vektorová rovnice:
$$\mathscr{P}(t)=C_0(t)P_0 + C_1(t)P_1 + C_2(t)P_2 + C_3(t)P_3,\ t\in[0,1]$$
Coonsovy polynomy
$C_0(t)=\frac{1}{6}(1-t)^3$
$C_1(t)=\frac{1}{6}(3t^3-6t^2+4)$
$C_2(t)=\frac{1}{6}(-3t^3+3t^2+3t+1)$
$C_3(t)=\frac{1}{6}t^3$
$C_1(t)=\frac{1}{6}(3t^3-6t^2+4)$
$C_2(t)=\frac{1}{6}(-3t^3+3t^2+3t+1)$
$C_3(t)=\frac{1}{6}t^3$
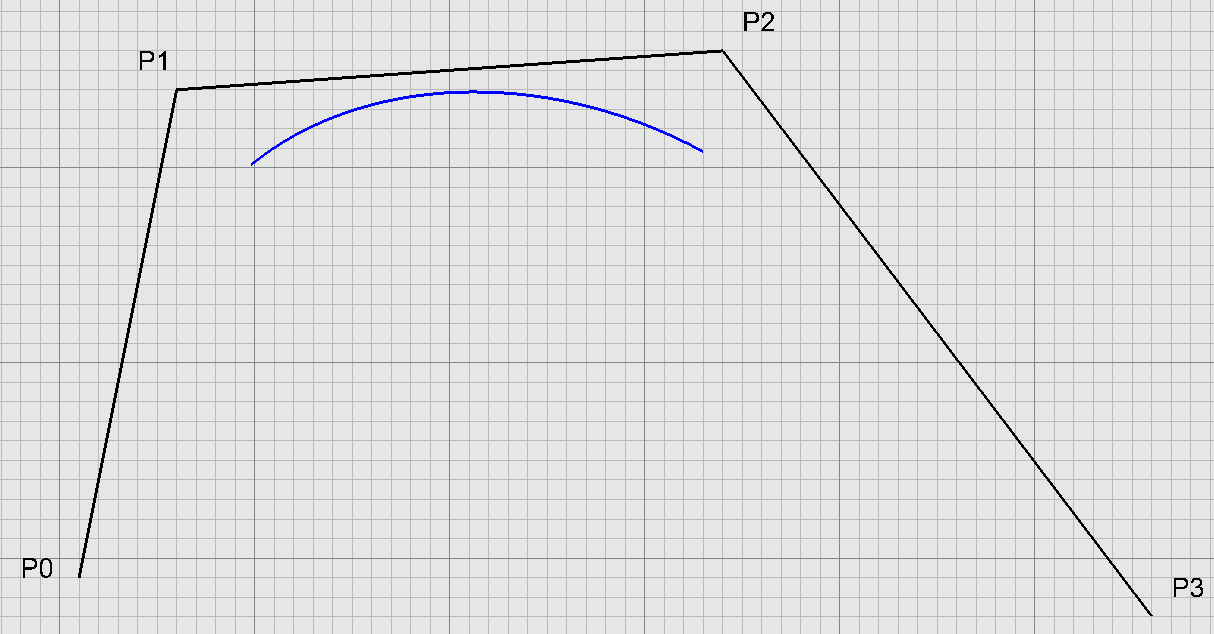
Vlastnosti Coonsovy kubiky
Coonsovy a Bernsteinovy polynomy - průběhy
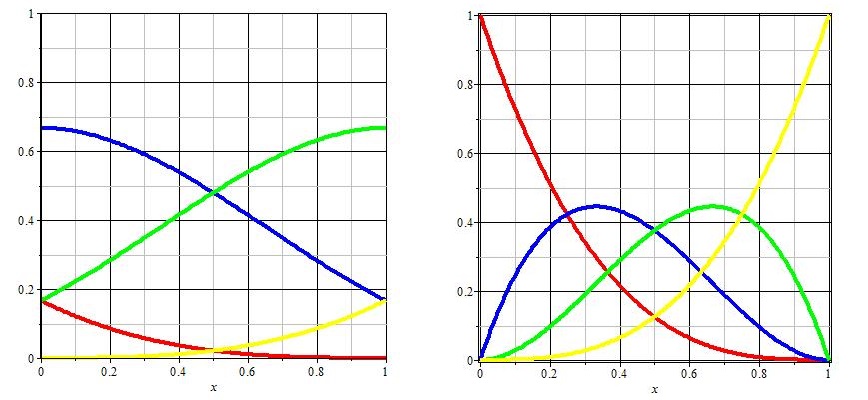
Počáteční bod křivky
$$\mathscr{P}(0)=\frac{1}{6}P_0 + \frac{2}{3}P_1 + \frac{1}{6}P_2\\ \Downarrow\\ \mathscr{P}(0)=P_1 + \frac{1}{6}(P_0-P_1) + \frac{1}{6}(P_2-P_1)\\ \Downarrow\\ \mathscr{P}(0)=P_1 + \frac{1}{2}(\frac{1}{3}\vec{P_1P_0}+\frac{1}{3}\vec{P_1P_2})$$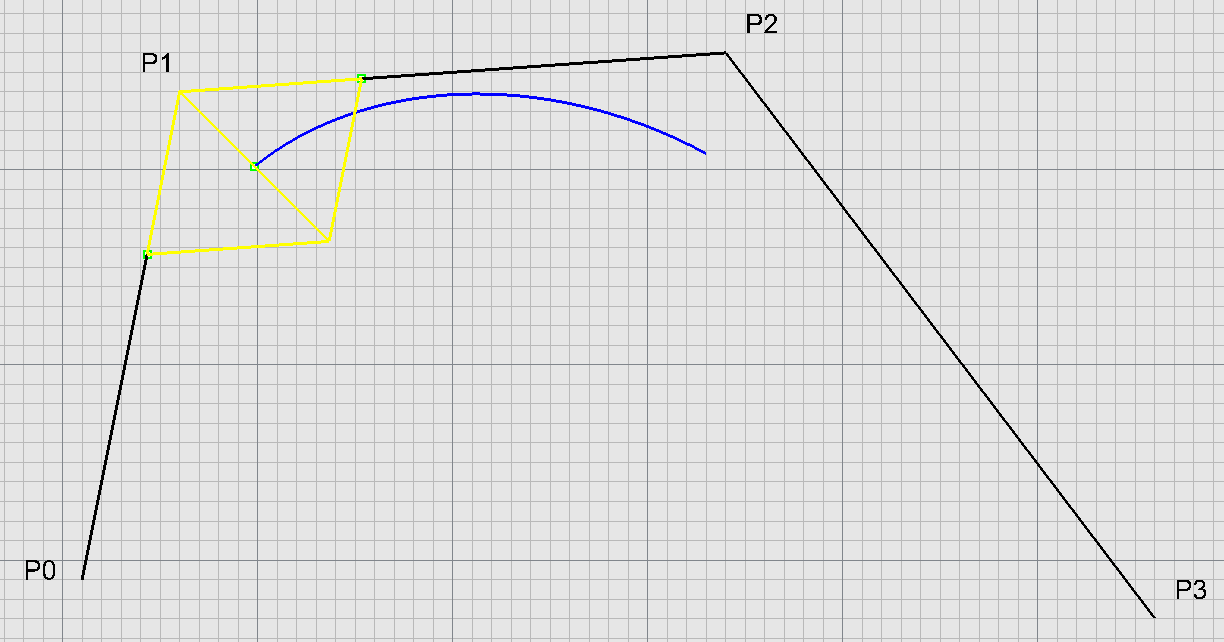
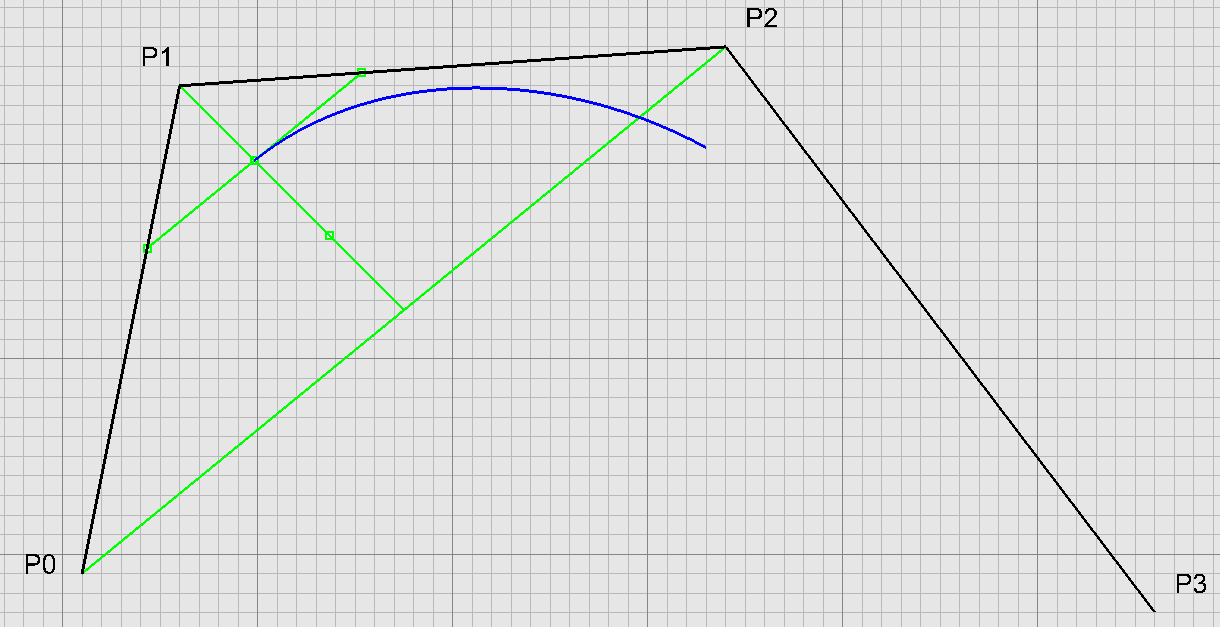 $\mathscr{P}(0)$ je tzv. antitěžiště trojúhelníka $P_0P_1P_2$
$\mathscr{P}(0)$ je tzv. antitěžiště trojúhelníka $P_0P_1P_2$
Koncový bod křivky
$$\mathscr{P}(1)=\frac{1}{6}P_1 + \frac{2}{3}P_2 + \frac{1}{6}P_3\\ \Downarrow\\ \mathscr{P}(1)=P_2 + \frac{1}{2}(\frac{1}{3}\vec{P_2P_1}+\frac{1}{3}\vec{P_2P_3})$$ $\mathscr{P}(1)$ je tzv. antitěžiště trojúhelníka $P_1P_2P_3$
$\mathscr{P}(1)$ je tzv. antitěžiště trojúhelníka $P_1P_2P_3$
Počáteční a koncový tečný vektor
derivace Coonsových polynomů:
$C'_0(t)=-\frac{1}{2}(1-t)^2$
$C'_1(t)=\frac{1}{2}(3t^2-4t)$
$C'_2(t)=\frac{1}{2}(-3t^2+2t+1)$
$C'_3(t)=\frac{1}{2}t$
$C'_1(t)=\frac{1}{2}(3t^2-4t)$
$C'_2(t)=\frac{1}{2}(-3t^2+2t+1)$
$C'_3(t)=\frac{1}{2}t$
$$\mathscr{P}'(0)=-\frac{1}{2}P_0 + \frac{1}{2}P_2 = \frac{1}{2}\vec{P_0P_2}$$
$$\mathscr{P}'(1)=-\frac{1}{2}P_1 + \frac{1}{2}P_3 = \frac{1}{2}\vec{P_1P_3}$$
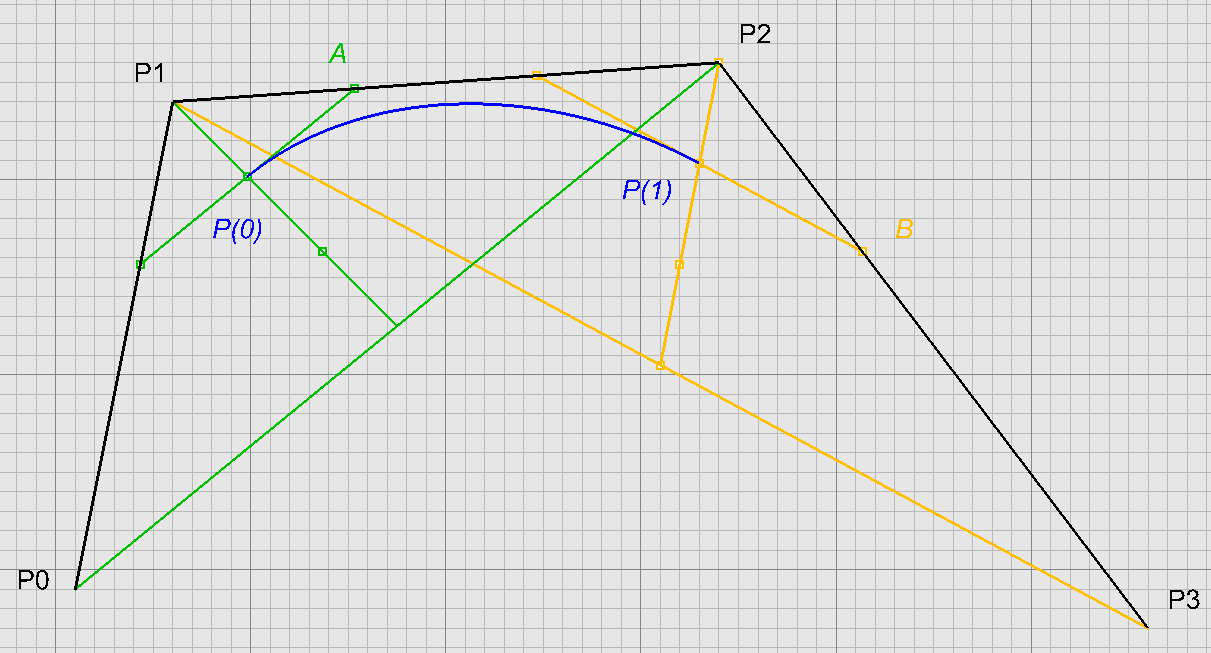
Vztah mezi Coonsovou a Bézierovou kubikou
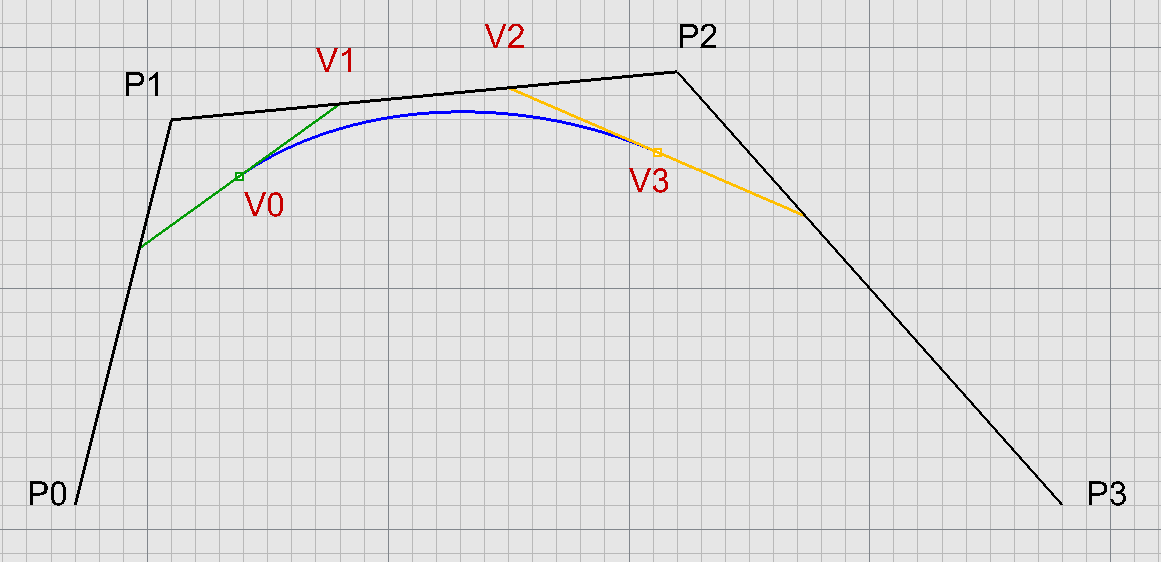
Vztahy mezi křivkami
Ferguson $\leftrightarrow$ Bézier $\leftrightarrow$ Coons
Fergusonova kubika - zadání
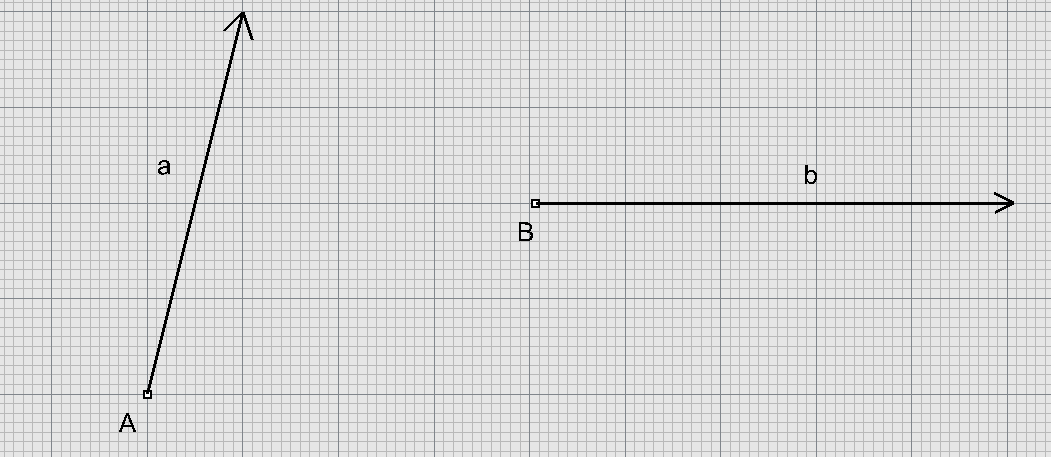
Ferguson $\Rightarrow$ Bézier
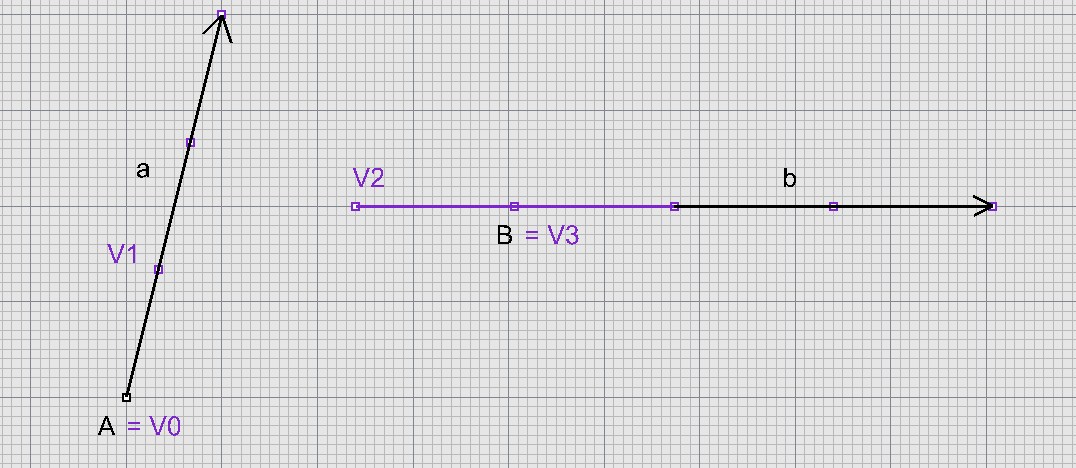
Bézierova kubika
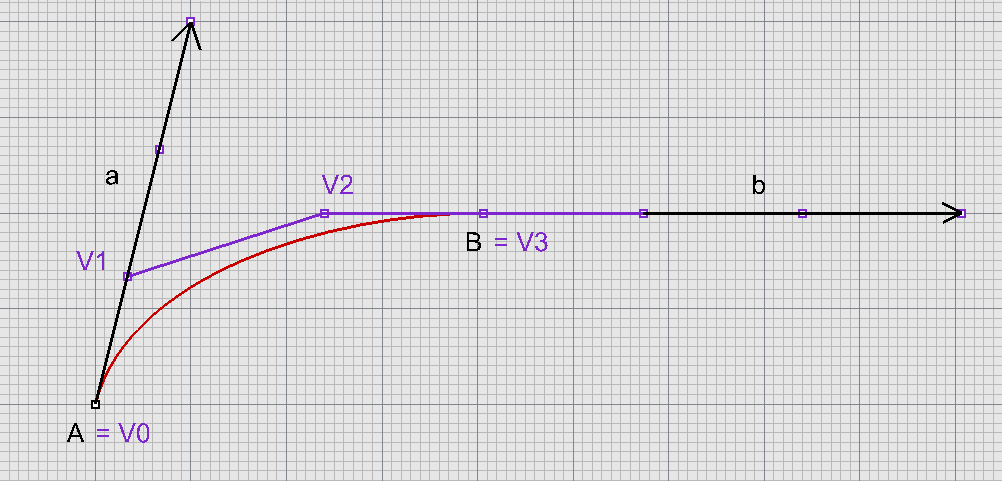
Bézier $\Rightarrow$ Coons

Napojování Coonsových kubik
$C^2$ spojité napojení
řídící polygon $P_0,P_1,P_2,P_3$ Coonsovy kubiky $\mathscr{P}(t)$
řídící polygon $R_0,R_1,R_2,R_3$ Coonsovy kubiky $\mathscr{R}(s)$
$C^0 \iff \frac{1}{6}P_1 + \frac{2}{3}P_2 + \frac{1}{6}P_3 = \frac{1}{6}R_0 + \frac{2}{3}R_1 + \frac{1}{6}R_2$
$C^1 \iff C^0 \land -\frac{1}{2}P_1+\frac{1}{2}P_3=-\frac{1}{2}R_0+\frac{1}{2}R_2$
$C^2 \iff C^1 \land P_1-2P_2+P_3=R_0-2R_1+R_2$
soustava 3 rovnic pro neznámé $R_0,R_1,R_2$ $\Rightarrow$ jediné řešení $R_0=P_1$, $R_1=P_2$, $R_2=P_3$
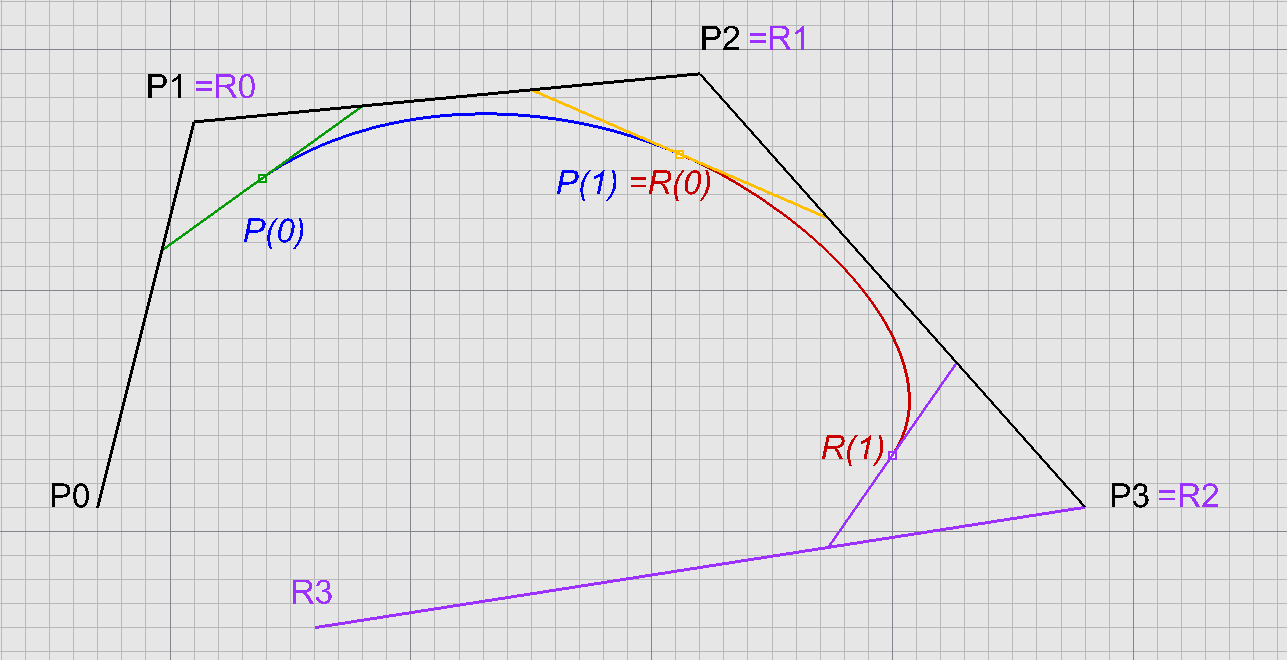
spline křivka
- interpolační vícesegmentová polynomiální křivka
B-spline křivka
- aproximační vícesegmentová křivka
- B (basis) - bázové funkce
- všechny segmenty napojeny se spojitostí min. $C^2$ (např. segmenty Bézierových kubik napojené s $C^2$ spojitostí)
- zobecněním B-spline křivky je NeUniformní Racionální B-Spline (NURBS)
Coonsův kubický B-spline
- aproximační vícesegmentová křivka třetího stupně, jejíž segmenty jsou Coonsovy kubiky napojené s $C^2$ spojitostí
v terminologii NURBS $\Rightarrow$ Uniformní neRacionální B-Spline 3. stupně
Coonsův kubický B-spline
Dáno: $P_0, P_1, ..., P_n$
jednotlivé segmenty jsou Coonsovy kubiky s řídícími polygony:
$P_0P_1P_2P_3$
$P_1P_2P_3P_4$
$\dots$
$P_{n-3}P_{n-2}P_{n-1}P_n$
$P_0P_1P_2P_3$
$P_1P_2P_3P_4$
$\dots$
$P_{n-3}P_{n-2}P_{n-1}P_n$
počet segmentů: n-2
Coonsův kubický B-spline
- otevřený
- uzavřený
Coonsův kubický B-spline otevřený
řídící polygon $P_0,P_1,P_2,\dots,P_6$
Coonsův kubický B-spline uzavřený
řídící polygon $P_0,P_1,P_2,P_3,P_4,P_0,P_1,P_2$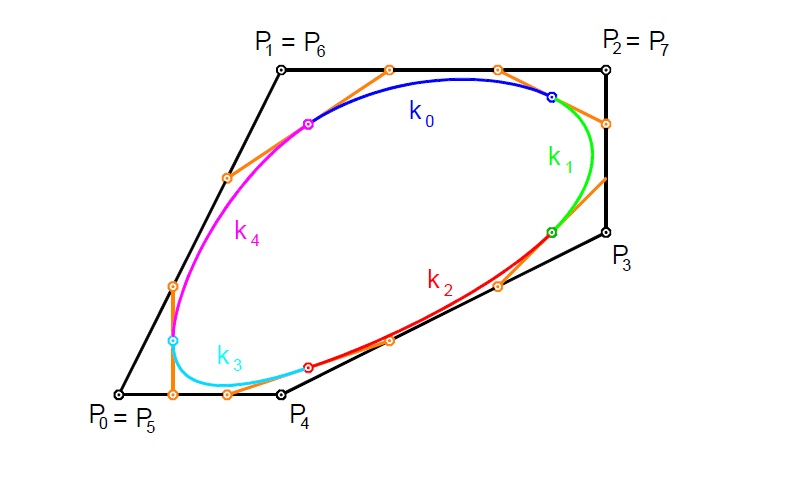
Ukotvená uniformní B-spline křivka třetího stupně
Dáno: $P_0, P_1, ..., P_n$
vícesegmentová B-spline kubika, prochází krajními řídícími body, ostatní body aproximuje
počet segmentů: n-2
Ukotvená kubika - 4 body
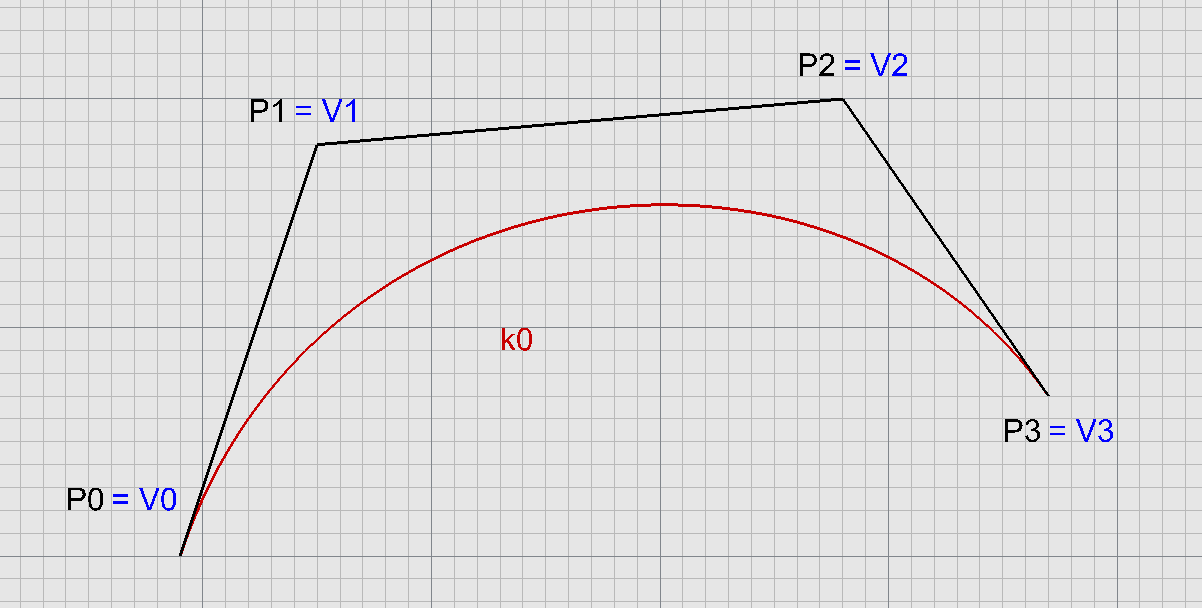
Ukotvená kubika - 5 bodů
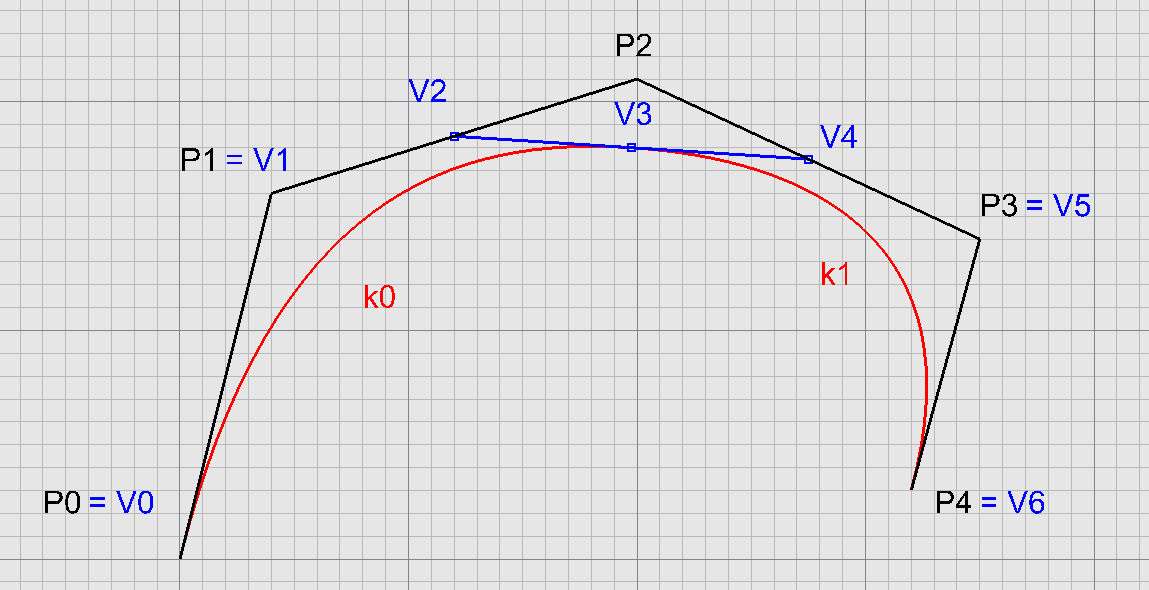
Ukotvená kubika - 6 bodů
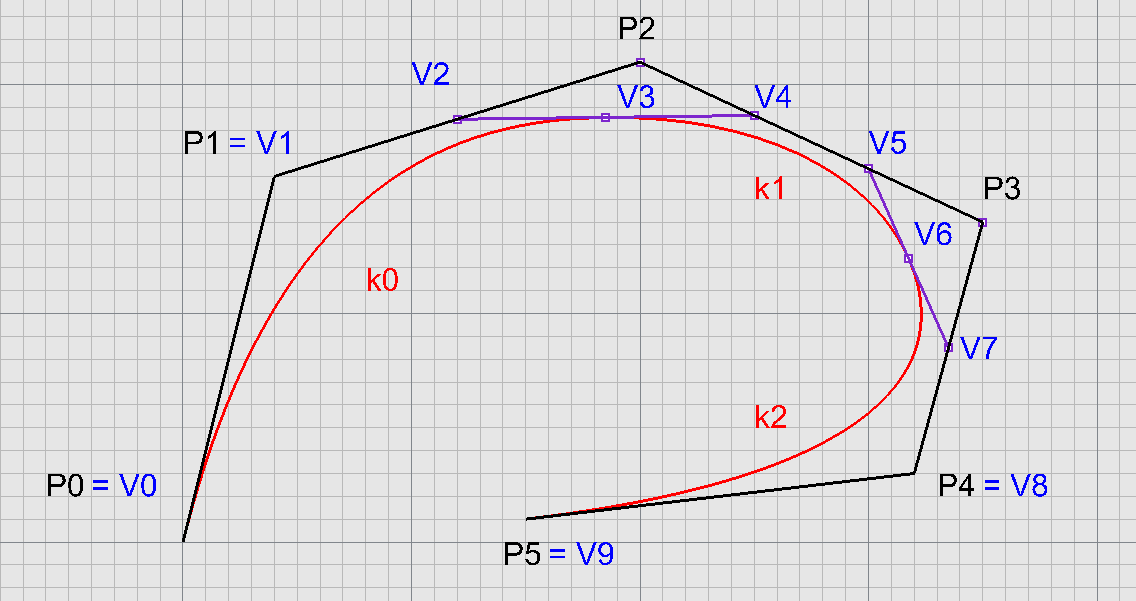
Ukotvená kubika - 10 bodů
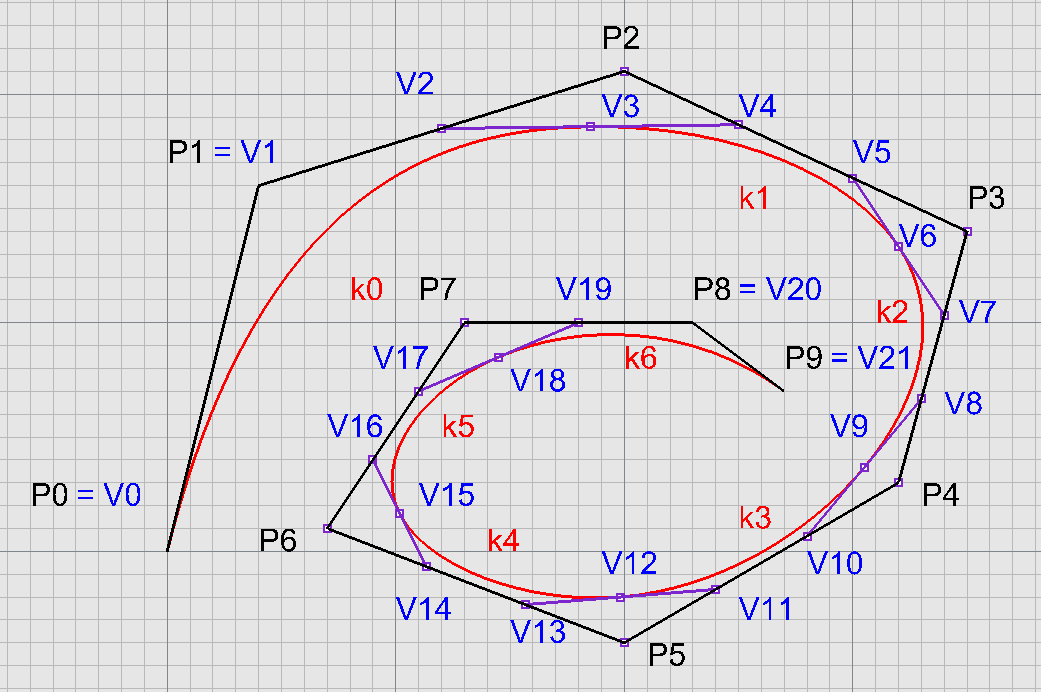
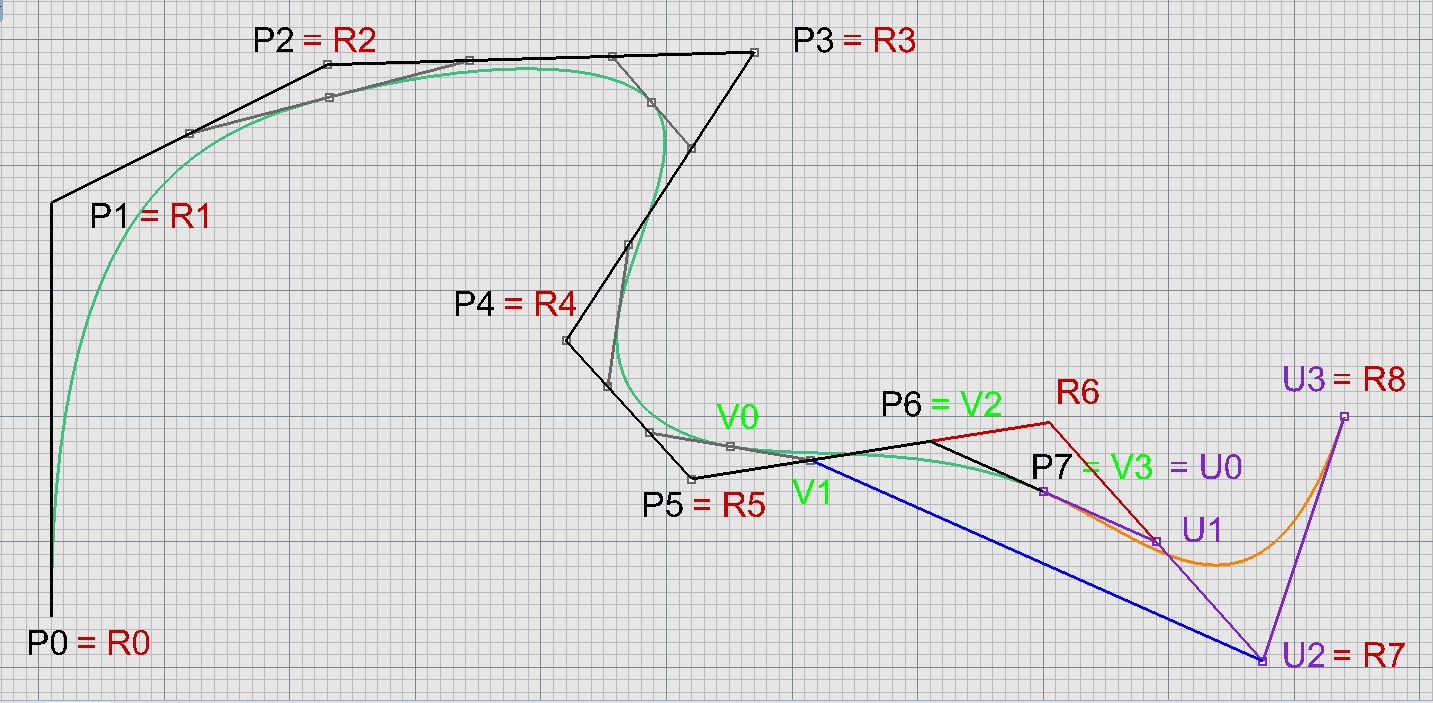
Ukotvená kubika - Coonsův kubický B-spline
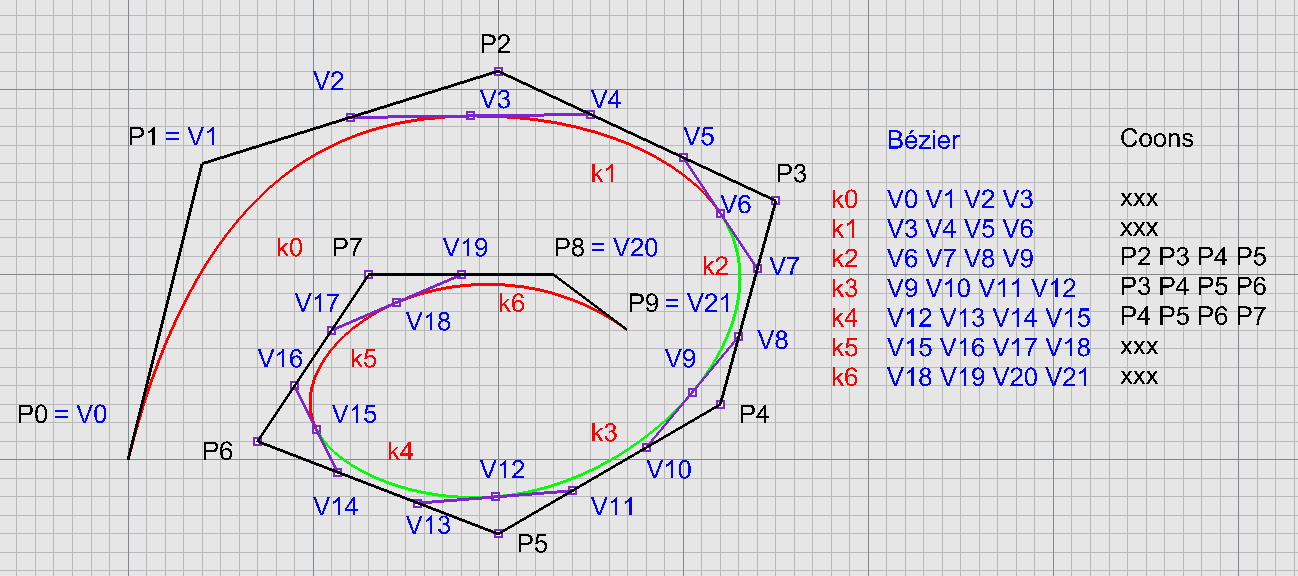
Vztahy mezi křivkami
Coonsův kubický B-spline $\leftrightarrow$ ukotvená kubika
Coonsův kubický B-spline (otevřený)
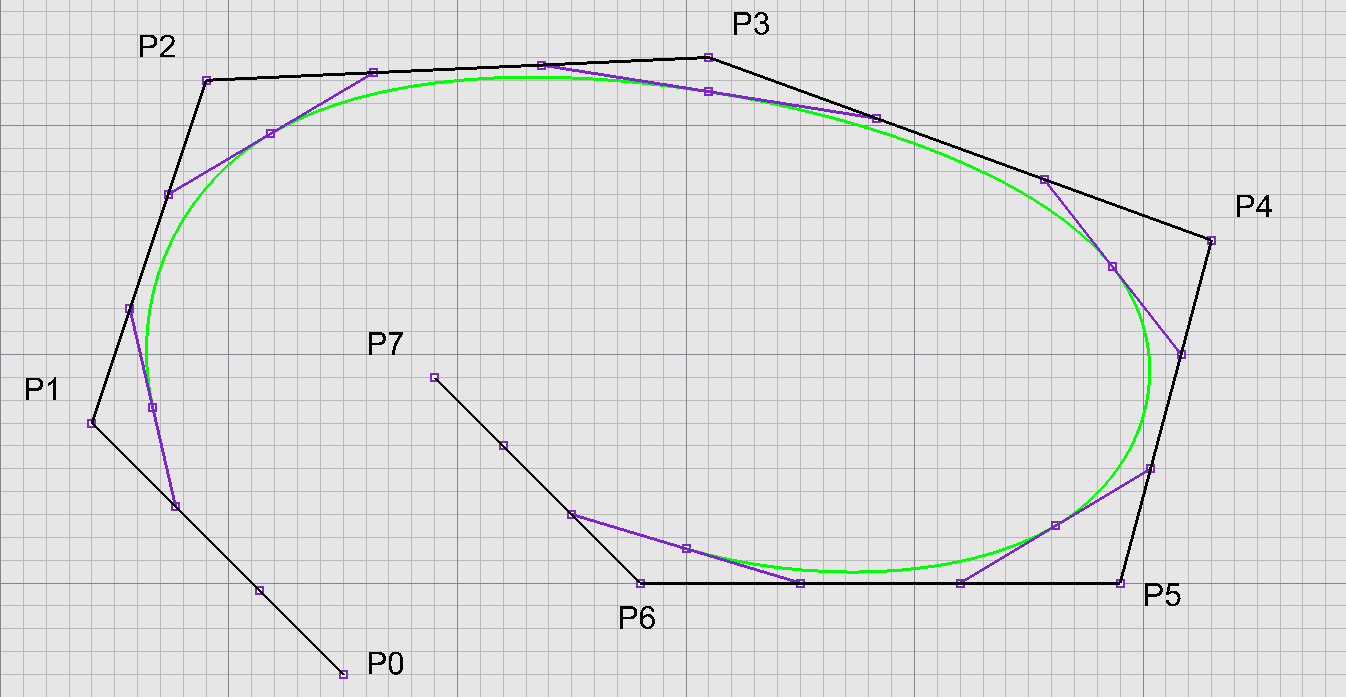
Coonsův kubický B-spline $\Rightarrow$ ukotvená kubika
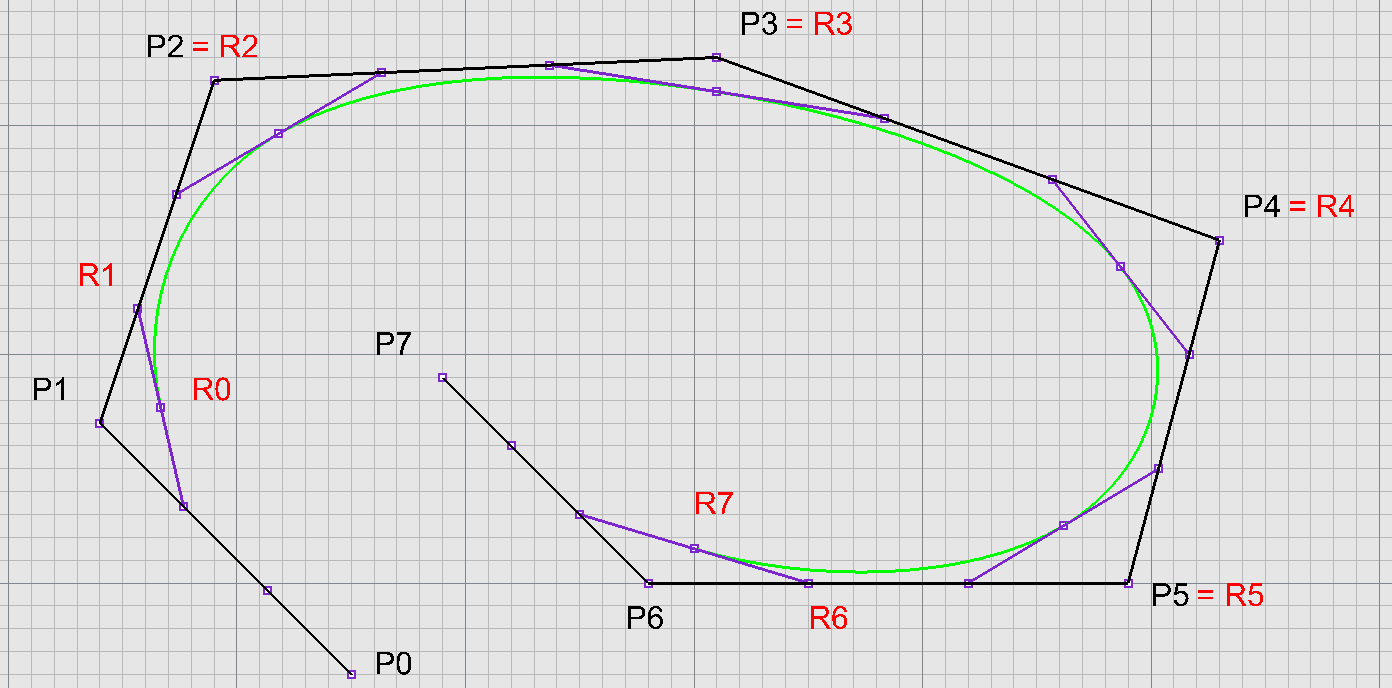
Ukotvená kubika - napojování
Ukotvená kubika - zadání
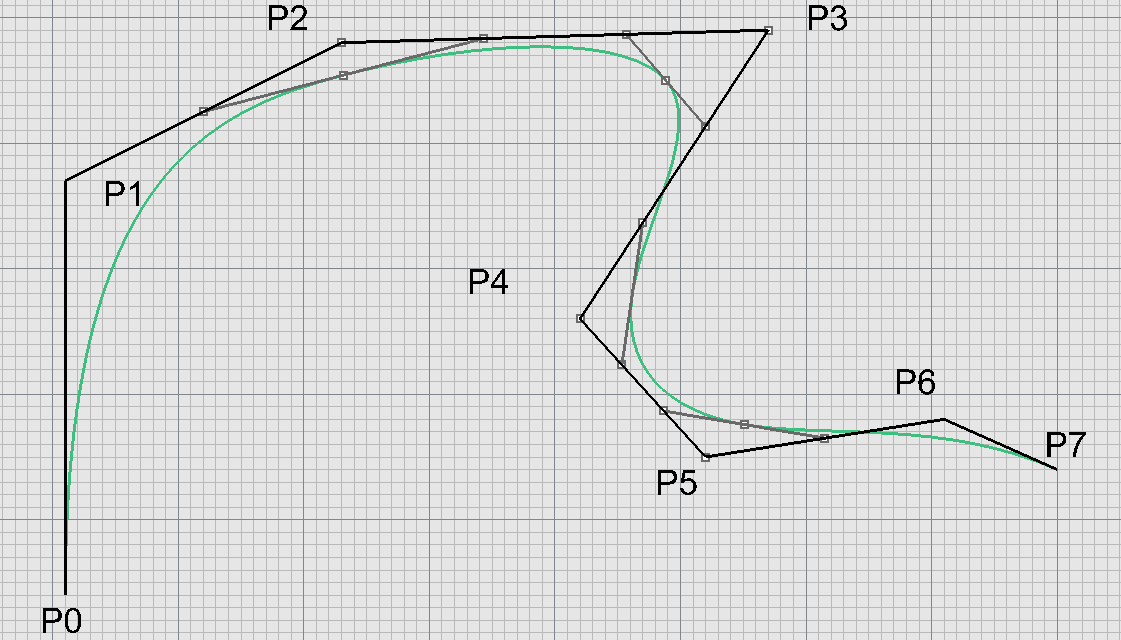
Poslední segment - Bézier
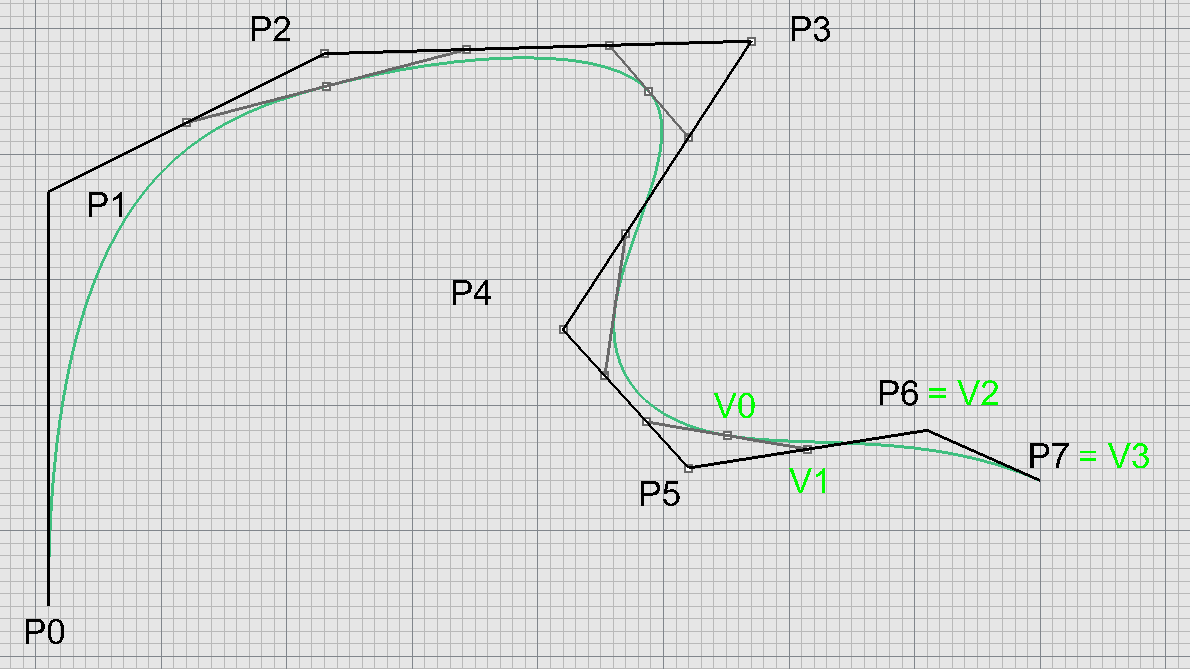
Napojení
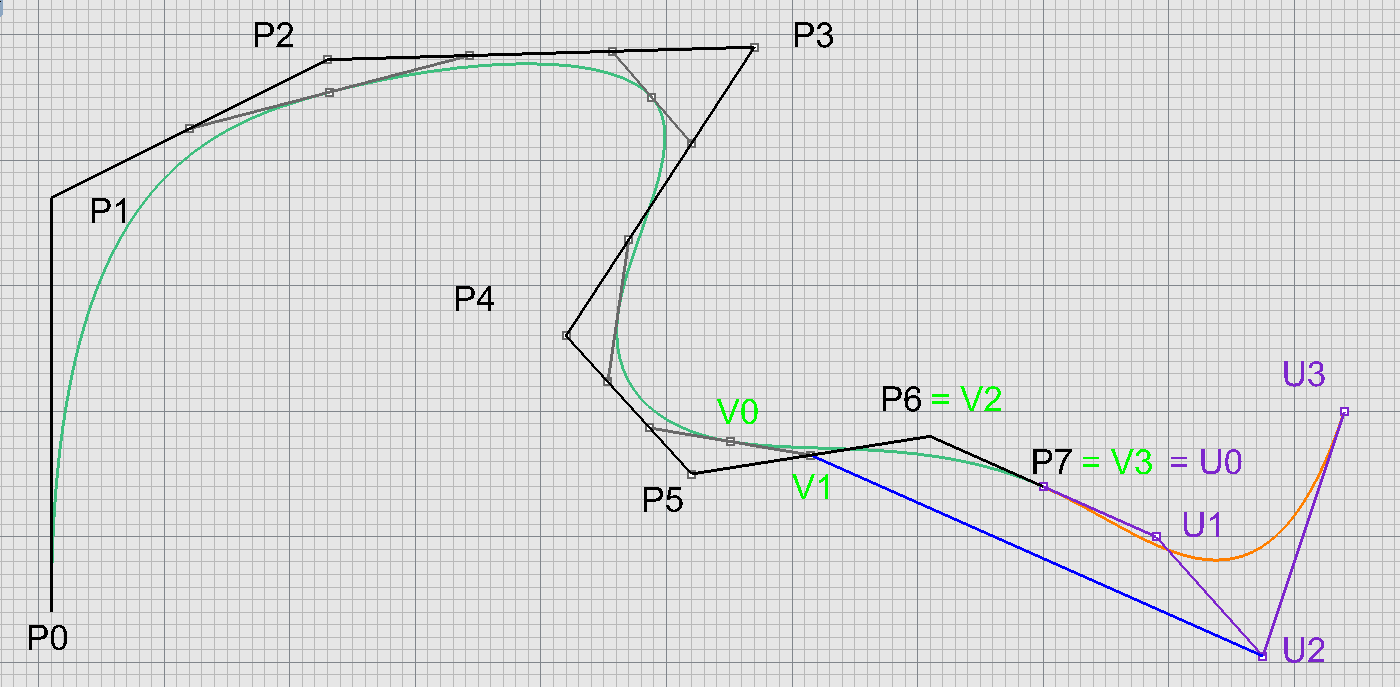
Nová ukotvená kubika