Počítačová grafika 22/23
Bézierova křivka (dokončení)
napojování křivek
napojování křivek
Vlastnosti Bézierových křivek
Bod křivky - počáteční a koncový
$$P(t)=\sum_{i=0}^{n}B_{i,n}(t)V_i,\ t\in[0,1]$$
počáteční bod křivky $\iff t=0$
koncový bod křivky $\iff t=1$
koncový bod křivky $\iff t=1$
Bernsteinovy polynomy - přehled
| $n$ | $1$ | $2$ | $3$ | $4$ | $\ldots$ |
|---|---|---|---|---|---|
| $B_{0,n}(t)$ | $1-t$ | $(1-t)^2$ | $(1-t)^3$ | $(1-t)^4$ | $\ldots$ |
| $B_{1,n}(t)$ | $t$ | $2t(1-t)$ | $3t(1-t)^2$ | $4t(1-t)^3$ | $\ldots$ |
| $B_{2,n}(t)$ | $\times$ | $t^2$ | $3t^2(1-t)$ | $6t^2(1-t)^2$ | $\ldots$ |
| $B_{3,n}(t)$ | $\times$ | $\times$ | $t^3$ | $4t^3(1-t)$ | $\ldots$ |
| $B_{4,n}(t)$ | $\times$ | $\times$ | $\times$ | $t^4$ | $\ldots$ |
| $\ldots$ | $\times$ | $\times$ | $\times$ | $\times$ | $\ldots$ |
Bernsteinovy polynomy
| n | $1$ | $2$ | $3$ | $4$ | ||||
|---|---|---|---|---|---|---|---|---|
| t | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| $B_{0,n}(t)$ | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| $B_{1,n}(t)$ | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| $B_{2,n}(t)$ | $\times$ | $\times$ | 0 | 1 | 0 | 0 | 0 | 0 |
| $B_{3,n}(t)$ | $\times$ | $\times$ | $\times$ | $\times$ | 0 | 1 | 0 | 0 |
| $B_{4,n}(t)$ | $\times$ | $\times$ | $\times$ | $\times$ | $\times$ | $\times$ | 0 | 1 |
Bernsteinovy polynomy - průběhy
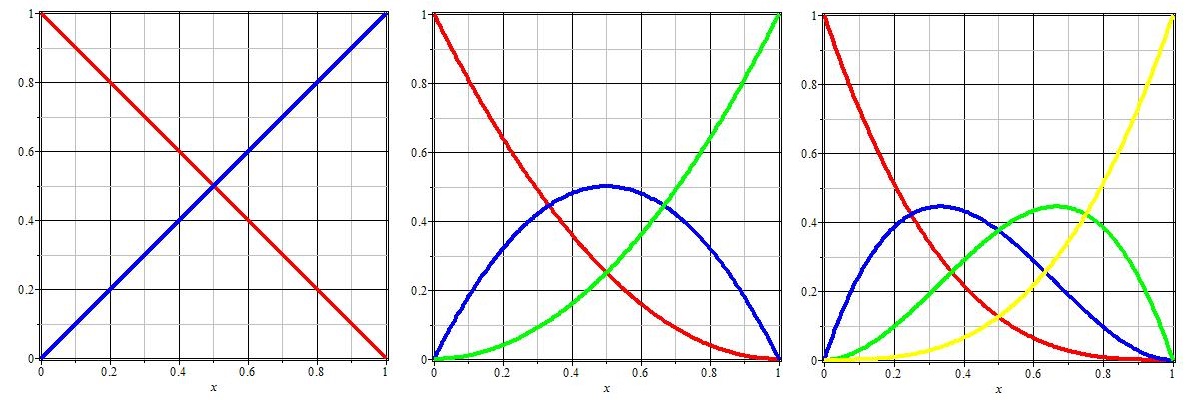
$\Rightarrow$ počáteční bod $P(0)=V_0$
$\Rightarrow$ koncový bod $P(1)=V_n$
$\Rightarrow$ koncový bod $P(1)=V_n$
Tečný vektor křivky - počáteční a koncový
$$P'(t)=\sum_{i=0}^{n}B_{i,n}'(t)V_i,\ t\in[0,1]$$
počáteční tečný vektor $\iff t=0$
koncový tečný vektor $\iff t=1$
koncový tečný vektor $\iff t=1$
lineární Bézierova křivka
| $i$ | $B_{i,1}(t)$ | $B_{i,1}'(t)$ | $B_{i,1}'(0)$ | $B_{i,1}'(1)$ |
|---|---|---|---|---|
| $0$ | $1-t$ | $-1$ | $-1$ | $-1$ |
| $1$ | $\phantom{1-}t$ | $\phantom{-}1$ | $\phantom{-}1$ | $\phantom{-}1$ |
$$P'(0)=-V_0+V_1=\vec{V_0V_1}$$ $$P'(1)=-V_0+V_1=\vec{V_0V_1}$$
kvadratická Bézierova křivka
| $i$ | $B_{i,2}(t)$ | $B_{i,2}'(t)$ | $B_{i,2}'(0)$ | $B_{i,2}'(1)$ |
|---|---|---|---|---|
| $0$ | $(1-t)^2$ | $-2(1-t)$ | $-2$ | $\phantom{-}0$ |
| $1$ | $2t(1-t)$ | $2(1-t)-2t$ | $\phantom{-}2$ | $-2$ |
| $2$ | $\phantom{-}t^2$ | $\phantom{-}2t$ | $\phantom{-}0$ | $\phantom{-}2$ |
$$P'(0)=-2V_0+2V_1=2\vec{V_0V_1}$$ $$P'(1)=-2V_1+2V_2=2\vec{V_1V_2}$$
kubická Bézierova křivka
| $i$ | $B_{i,3}(t)$ | $B_{i,3}'(t)$ | $B_{i,3}'(0)$ | $B_{i,3}'(1)$ |
|---|---|---|---|---|
| $0$ | $(1-t)^3$ | $-3(1-t)^2$ | $-3$ | $\phantom{-}0$ |
| $1$ | $3t(1-t)^2$ | $3(1-t)^2-6t(1-t)$ | $\phantom{-}3$ | $\phantom{-}0$ |
| $2$ | $3t^2(1-t)$ | $6t(1-t)-3t^2$ | $\phantom{-}0$ | $-3$ |
| $3$ | $\phantom{-}t^3$ | $\phantom{-}3t^2$ | $\phantom{-}0$ | $\phantom{-}3$ |
$$P'(0)=-3V_0+3V_1=3\vec{V_0V_1}$$ $$P'(1)=-3V_2+3V_3=3\vec{V_2V_3}$$
Bézierova křivka n-tého stupně
$P'(0)=n\vec{V_0V_1}$
$P'(1)=n\vec{V_{n-1}V_{n}}$
$P(0)=V_1$
$P(1)=V_n$
$P'(1)=n\vec{V_{n-1}V_{n}}$
$P(0)=V_1$
$P(1)=V_n$
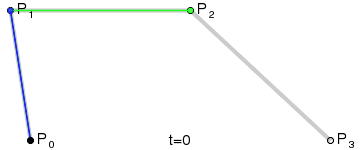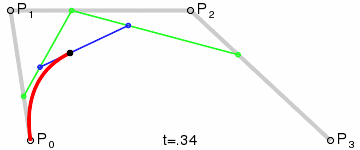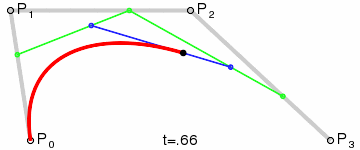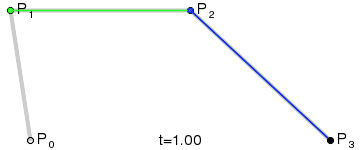
de Casteljau algoritmus
de Casteljau algoritmus
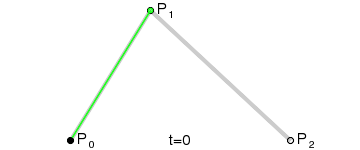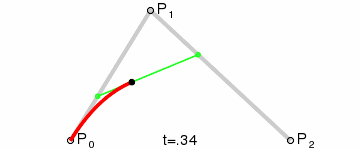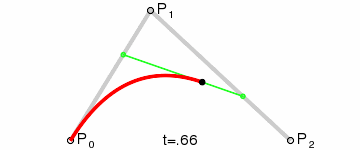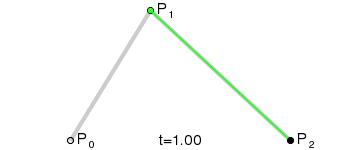
lineární křivka
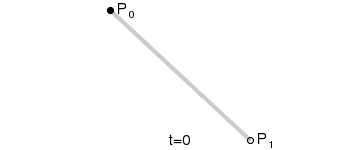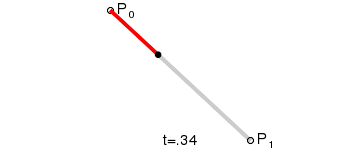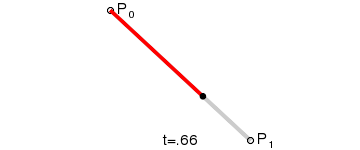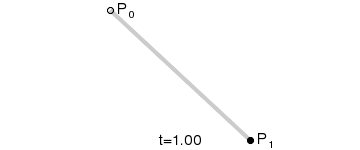
de Casteljau algoritmus
kvadratická křivka
de Casteljau algoritmus
kubická křivka
de Casteljau algoritmus
křivka 4. stupně
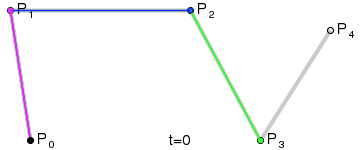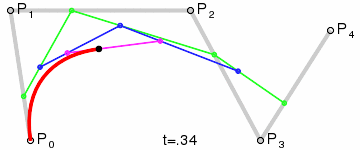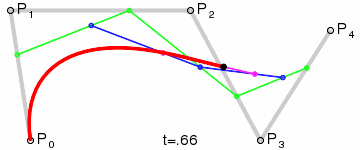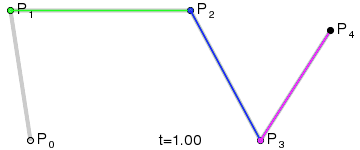
de Casteljau algoritmus
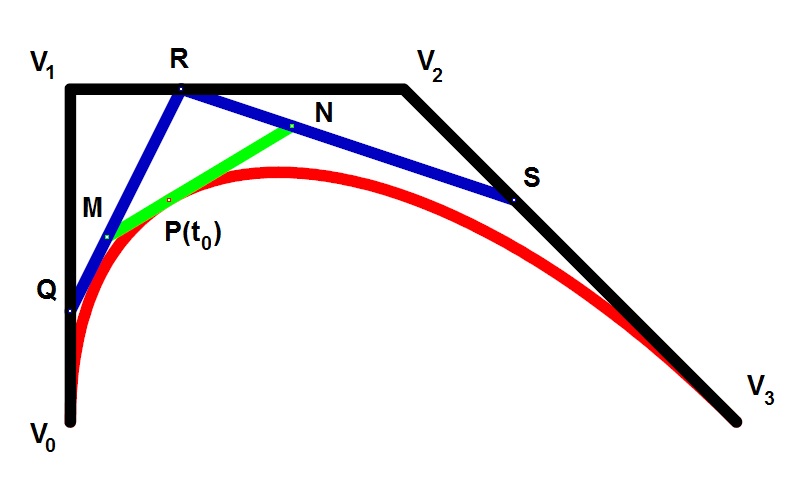
$$P'(t_0)=n\vec{MN}$$
Napojování křivek
- spojitost geometrická - $G^n$
- spojitost parametrická - $C^n$
Geometrická spojitost napojení 2 křivek
$G^0 \iff$ společný bod
$G^1 \iff G^0 + $stejná tečna ve společném bodě
$G^2 \iff G^1 +$ stejná křivost ve společném bodě
$G^1 \iff G^0 + $stejná tečna ve společném bodě
$G^2 \iff G^1 +$ stejná křivost ve společném bodě
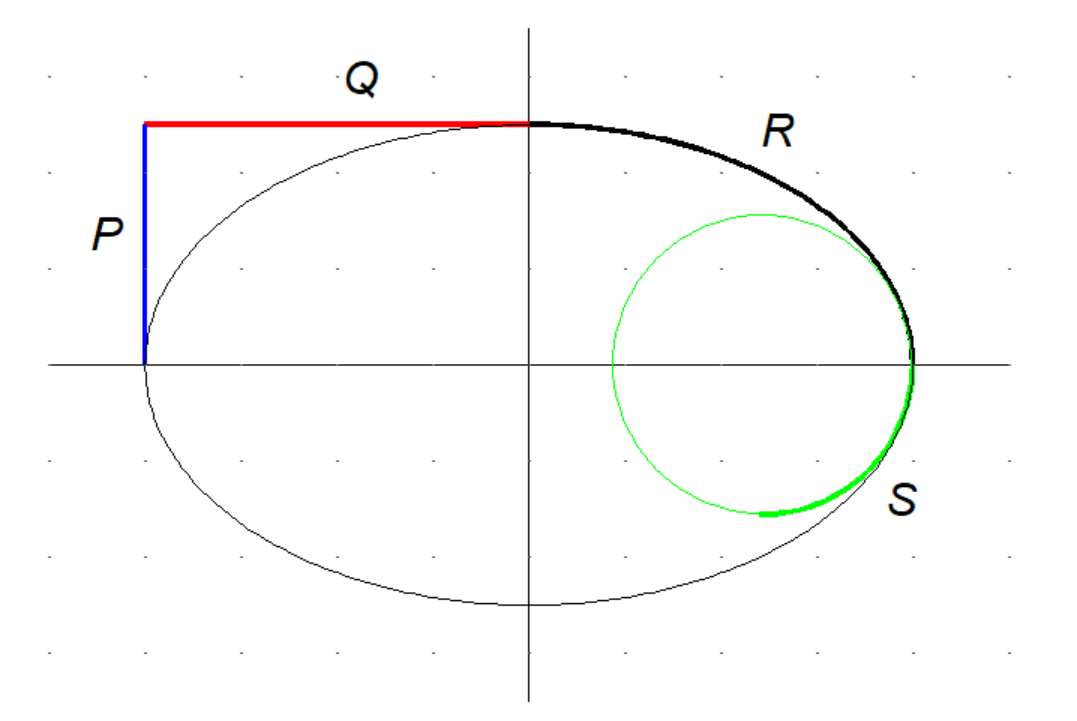
Parametrická spojitost napojení 2 křivek
Pro dvě uniformní křivky $P(t)$ a $Q(s)$:
$C^0 \iff P(1)=Q(0)$
$C^1 \iff C^0 \land P'(1)=Q'(0)$
$C^2 \iff C^1 \land P''(1)=Q''(0)$
...
$C^1 \iff C^0 \land P'(1)=Q'(0)$
$C^2 \iff C^1 \land P''(1)=Q''(0)$
...
spojitost parametrická $\Rightarrow$ spojitost geometrická
Napojování Bézierových křivek - kubik
Křivka $P(t)$: řídící polygon $V_i, i=0,1,2,3$
Křivka $Q(s)$: řídící polygon $U_i, i=0,1,2,3$
Odvození podmínek pro umístění řídících bodů $U_i$, tak aby napojení bylo $C^0, C^1, C^2$.
Bernsteinovy polynomy
| $t=0$ | $t=1$ | |
| $B_{0,n}(t)=(1-t)^3$ | $1$ | $0$ |
| $B_{1,n}(t)=3t(1-t)^2$ | $0$ | $0$ |
| $B_{2,n}(t)=3t^2(1-t)$ | $0$ | $0$ |
| $B_{3,n}(t)=t^3$ | $0$ | $1$ |
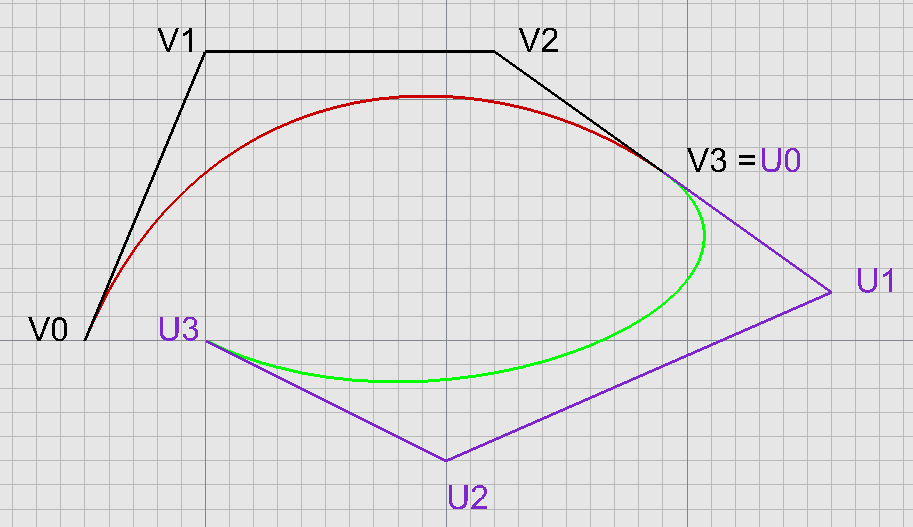
Spojitost napojení $C^0$
$$P(1)=Q(0) \Rightarrow \color{blue}{U_0=V_3}$$
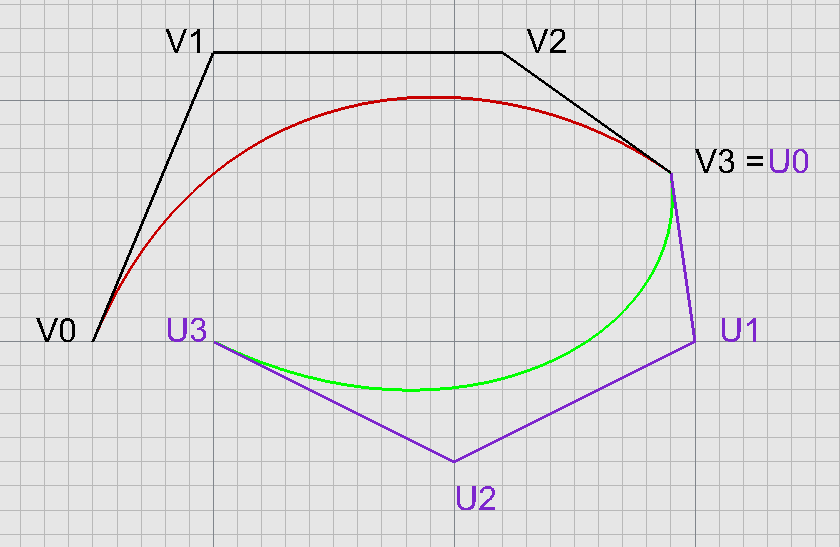
Bernsteinovy polynomy - první derivace
| $t=0$ | $t=1$ | |
| $B'_{0,n}(t)=3(1-t)^2$ | $-3$ | $\phantom{-}0$ |
| $B'_{1,n}(t)=3(1-t)(1-3t)$ | $\phantom{-}3$ | $\phantom{-}0$ |
| $B'_{2,n}(t)=3t(2-3t)$ | $\phantom{-}0$ | $-3$ |
| $B'_{3,n}(t)=3t^2$ | $\phantom{-}0$ | $\phantom{-}3$ |
Spojitost napojení $C^1$
$C^0 \land P'(1)=Q'(0)$
$V_3-V_2 = U_1-U_0 \Rightarrow \color{blue}{U_1=U_0+\vec{V_2V_3}}$
Bernsteinovy polynomy - druhá derivace
| $t=0$ | $t=1$ | |
| $B''_{0,n}(t)=6(1-t)$ | $\phantom{-1}6$ | $\phantom{-1}0$ |
| $B''_{1,n}(t)=3(6t-4)$ | $-12$ | $\phantom{-1}6$ |
| $B''_{2,n}(t)=-3(6t-2)$ | $\phantom{-1}6$ | $-12$ |
| $B''_{3,n}(t)=6t$ | $\phantom{-1}0$ | $\phantom{-1}6$ |
Spojitost napojení $C^2$
$C^1 \land P''(1)=Q''(0)$
$6V_1-12V_2+6V_3=6U_0-12U_1+6U_2 \Rightarrow \color{blue}{U_2=V_1+4\vec{V_2V_3}}$

Grafy křivostí napojených kubik
(Rhino)
$G^0$
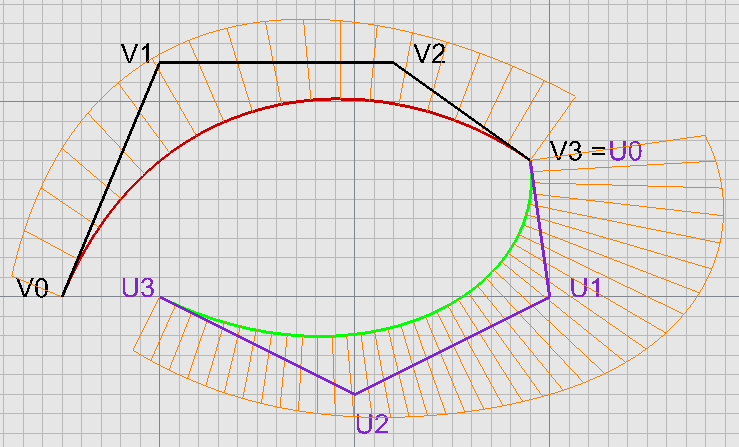
$G^1$
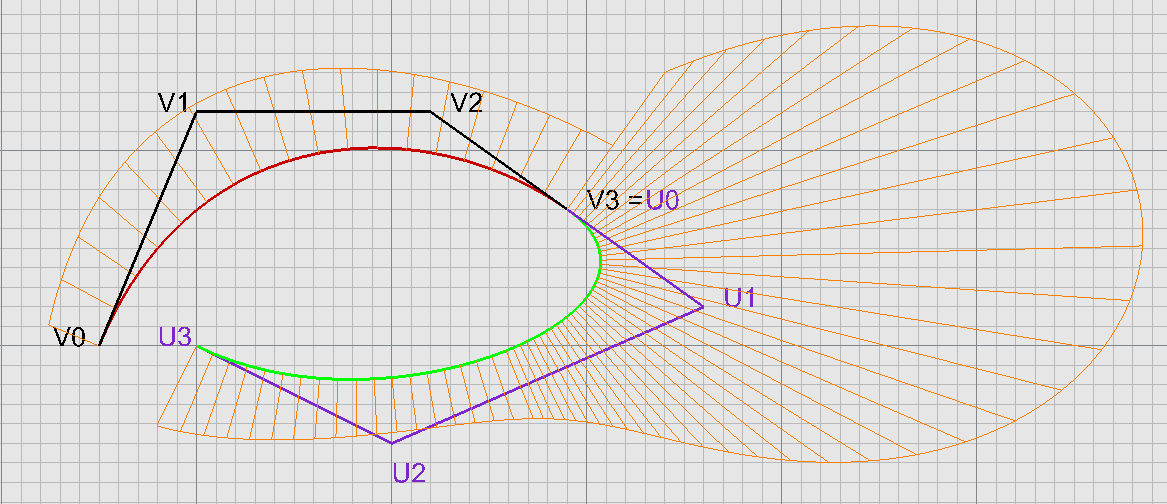
$G^2$
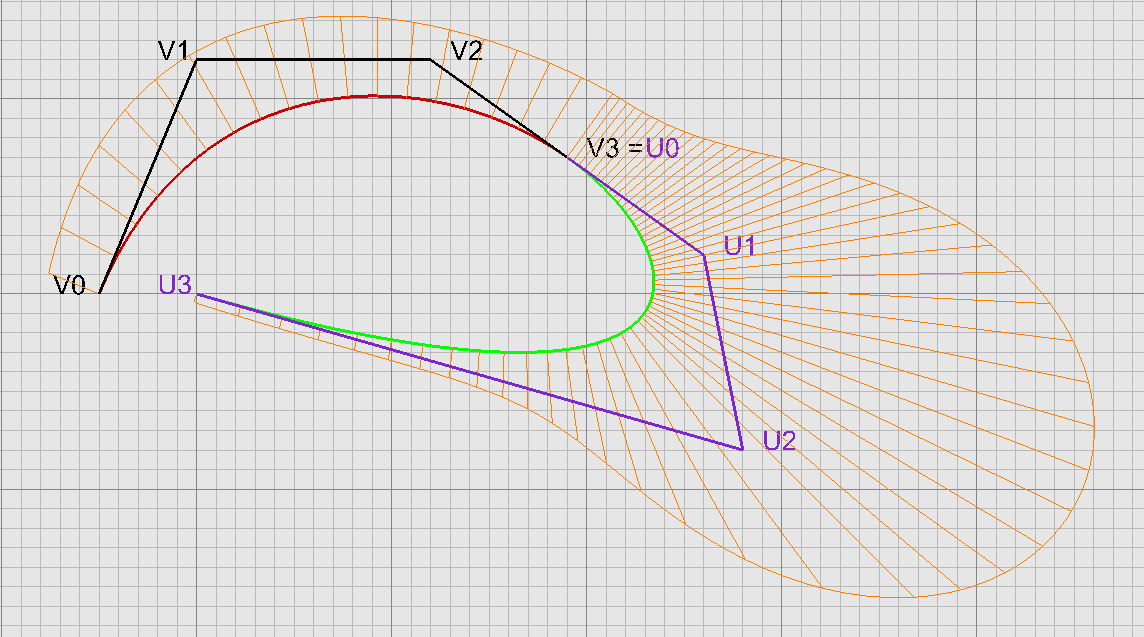
Napojování Bézierových křivek rozdílných stupňů
Křivka $P(t)$: řídící polygon $V_i, i=0,1,2,3$
Křivka $Q(s)$: řídící polygon $U_i, i=0,1,\dots$
Odvození podmínek pro umístění řídících bodů $U_i$, tak aby napojení bylo $C^0, C^1, C^2, (C^3)$.
Bernsteinovy polynomy - přehled
| $n$ | $1$ | $2$ | $3$ | $4$ |
|---|---|---|---|---|
| $B_{0,n}$ | $1-t$ | $(1-t)^2$ | $(1-t)^3$ | $(1-t)^4$ |
| $B_{1,n}$ | $t$ | $2t(1-t)$ | $3t(1-t)^2$ | $4t(1-t)^3$ |
| $B_{2,n}$ | $\times$ | $t^2$ | $3t^2(1-t)$ | $6t^2(1-t)^2$ |
| $B_{3,n}$ | $\times$ | $\times$ | $t^3$ | $4t^3(1-t)$ |
| $B_{4,n}$ | $\times$ | $\times$ | $\times$ | $t^4$ |
Bernsteinovy polynomy - první derivace
| n | $1$ | $2$ | $3$ | $4$ | ||||
|---|---|---|---|---|---|---|---|---|
| t | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| $B'_{0,n}$ | -1 | -1 | -2 | 0 | -3 | 0 | -4 | 0 |
| $B'_{1,n}$ | 1 | 1 | 2 | -2 | 3 | 0 | 4 | 0 |
| $B'_{2,n}$ | $\times$ | $\times$ | 0 | 2 | 0 | -3 | 0 | 0 |
| $B'_{3,n}$ | $\times$ | $\times$ | $\times$ | $\times$ | 0 | 3 | 0 | -4 |
| $B'_{4,n}$ | $\times$ | $\times$ | $\times$ | $\times$ | $\times$ | $\times$ | 0 | 4 |
Bernsteinovy polynomy - druhá derivace
| n | $1$ | $2$ | $3$ | $4$ | ||||
|---|---|---|---|---|---|---|---|---|
| t | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| $B''_{0,n}$ | 0 | 0 | 2 | 2 | 6 | 0 | 12 | 0 |
| $B''_{1,n}$ | 0 | 0 | -4 | -4 | -12 | 6 | -24 | 0 |
| $B''_{2,n}$ | $\times$ | $\times$ | 2 | 2 | 6 | -12 | 12 | 12 |
| $B''_{3,n}$ | $\times$ | $\times$ | $\times$ | $\times$ | 0 | 6 | 0 | -24 |
| $B''_{4,n}$ | $\times$ | $\times$ | $\times$ | $\times$ | $\times$ | $\times$ | 0 | 12 |
Spojitost napojení $C^1$
napojení lineární Bézierovy křivky:
$U_0=V_3 \land U_1=V_3+3\vec{V_2V_3}$
$U_0=V_3 \land U_1=V_3+3\vec{V_2V_3}$
napojení kvadratické B. křivky:
$U_0=V_3 \land U_1=V_3+\frac{3}{2}\vec{V_2V_3}$
$U_0=V_3 \land U_1=V_3+\frac{3}{2}\vec{V_2V_3}$
napojení kubické B. křivky:
$U_0=V_3 \land U_1=V_3+\vec{V_2V_3}$
$U_0=V_3 \land U_1=V_3+\vec{V_2V_3}$
napojení kvartické B. křivky:
$U_0=V_3 \land U_1=V_3+\frac{3}{4}\vec{V_2V_3}$
$U_0=V_3 \land U_1=V_3+\frac{3}{4}\vec{V_2V_3}$
Spojitost napojení $C^2$
napojení kvadratické B. křivky:
$U_0=V_3 \land U_1=V_3+\frac{3}{2}\vec{V_2V_3}\land U_2=V_1+2\vec{V_2V_1}+7\vec{V_2V_3}$
$U_0=V_3 \land U_1=V_3+\frac{3}{2}\vec{V_2V_3}\land U_2=V_1+2\vec{V_2V_1}+7\vec{V_2V_3}$
napojení kubické B. křivky:
$U_0=V_3 \land U_1=V_3+\vec{V_2V_3}\land U_2=V_1+4\vec{V_2V_3}$
$U_0=V_3 \land U_1=V_3+\vec{V_2V_3}\land U_2=V_1+4\vec{V_2V_3}$
napojení kvartické B. křivky:
$U_0=V_3 \land U_1=V_3+\frac{3}{4}\vec{V_2V_3}\land U_2=V_1+\frac{5}{2}\vec{V_2V_3}+\frac{1}{2}\vec{V_1V_3}$
$U_0=V_3 \land U_1=V_3+\frac{3}{4}\vec{V_2V_3}\land U_2=V_1+\frac{5}{2}\vec{V_2V_3}+\frac{1}{2}\vec{V_1V_3}$