Konstruktivní geometrie 2023/24
Průniky rotačních ploch
Obecný postup konstrukce průnikové křivky
Dány rotační plochy $\kappa$ a $\kappa'$.
- volba pomocné plochy $\kappa^{\ast}$
- průnik $\kappa$ a $\kappa^{\ast}$ $\rightarrow$ křivka $k$
- průnik $\kappa'$ a $\kappa^{\ast}$ $\rightarrow$ křivka $k'$
- průsečík(y) $k$ a $k'$ $\rightarrow$ body průniku $X, Y$
- nová volba pomocné plochy $\kappa^{\ast}$ ...
Typ pomocné plochy $\kappa^{\ast}$ závisí na vzájemné poloze os daných rotačních ploch.
Pouze případy os totožných, rovnoběžných, různoběžných - mimoběžnými osami se zabývat nebudeme!
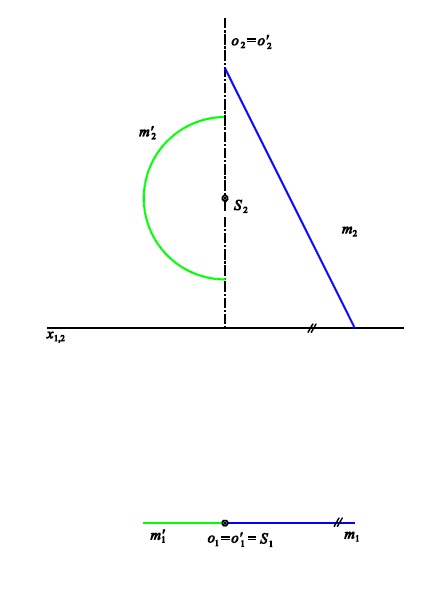
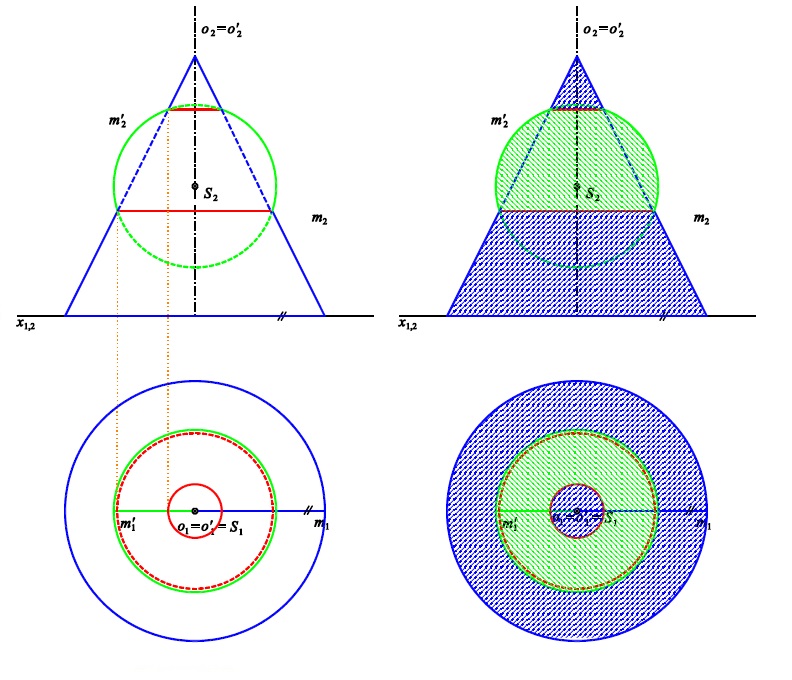
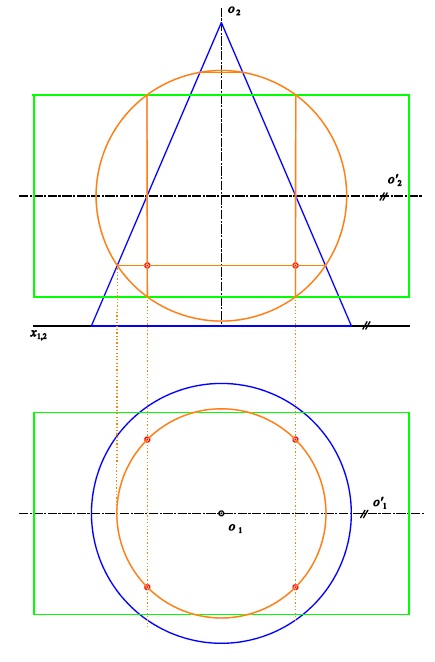
Osy totožné
Pomocná plocha $\kappa^{\ast}$ je rovina kolmá ke společné ose
Příklad 1: Sestrojte průnikovou křivku rotačních ploch $\kappa$ (osa $o$, hlavní polomeridián $m$)
a $\kappa'$ (osa $o'$, hlavní polomeridián $m'$).
a $\kappa'$ (osa $o'$, hlavní polomeridián $m'$).
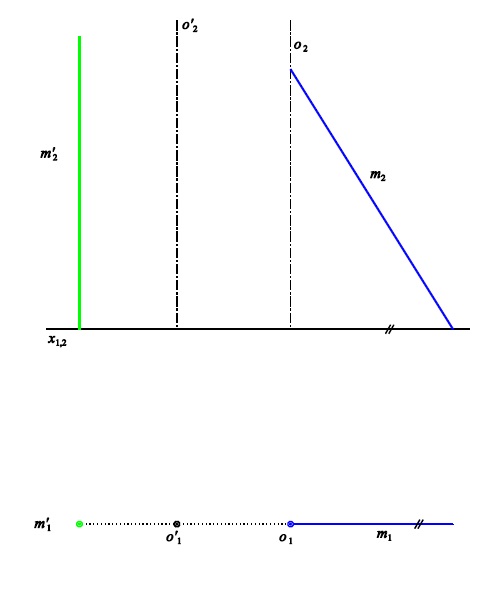
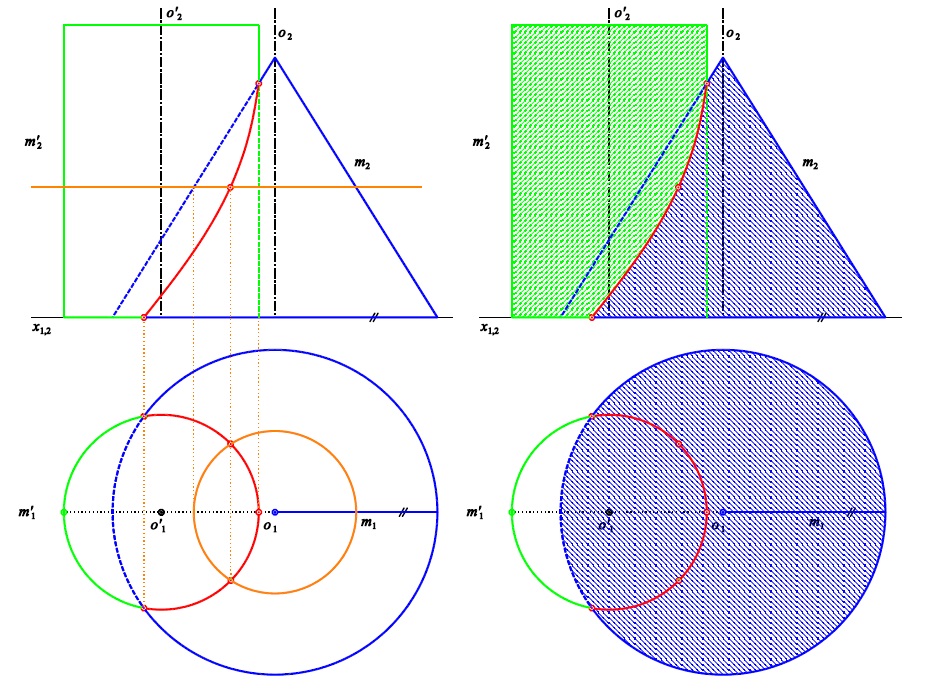
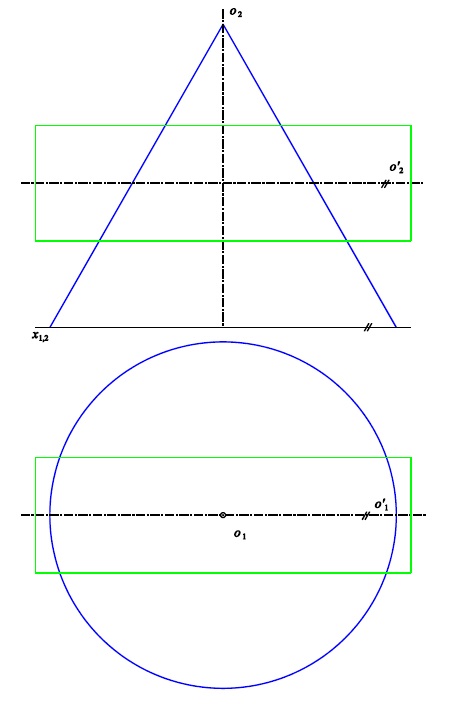
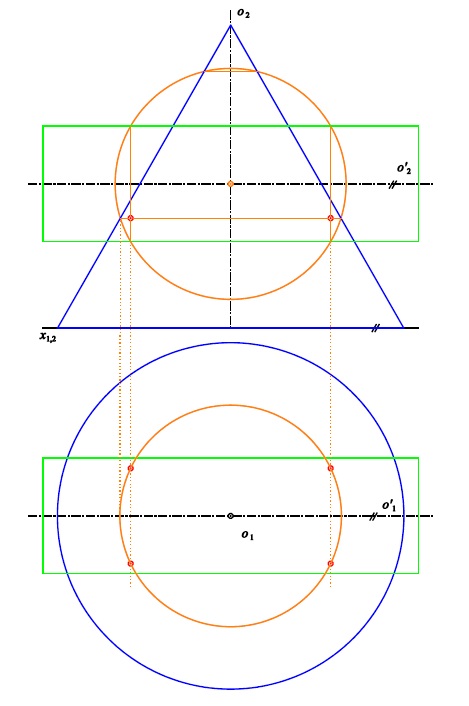
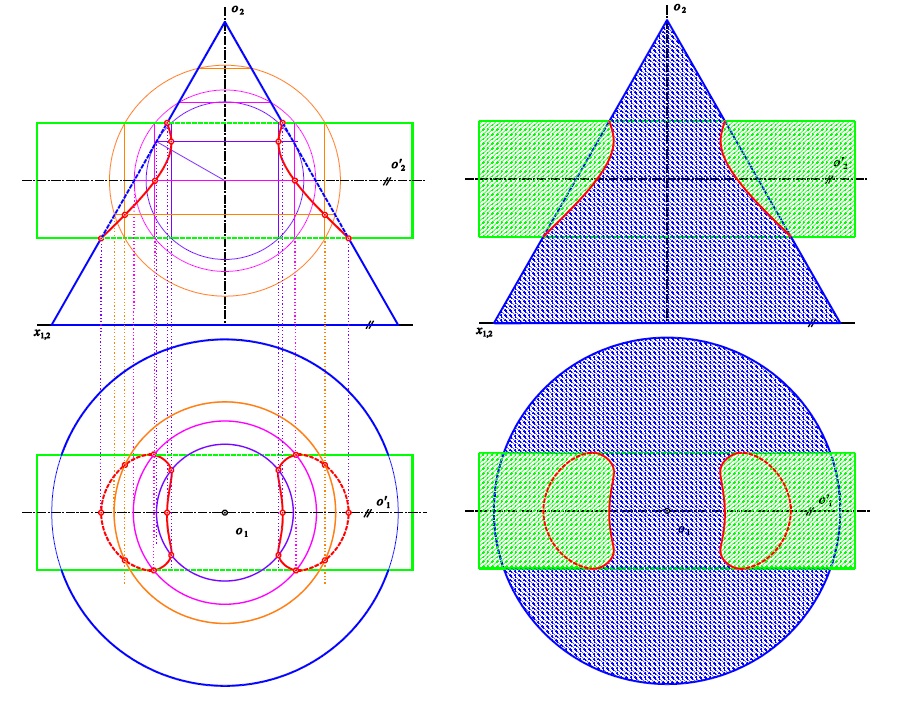
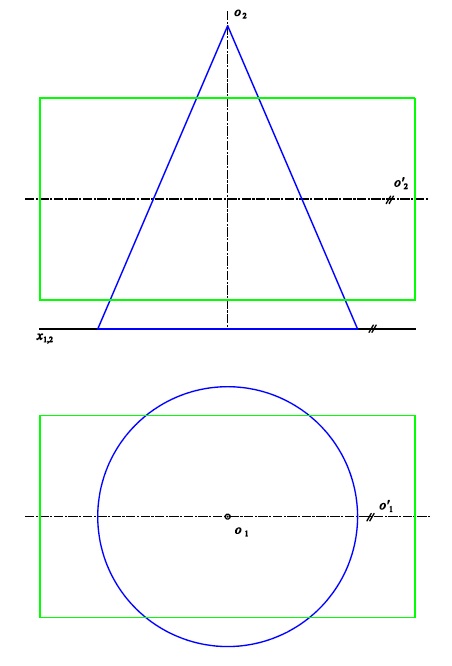
Osy rovnoběžné
Pomocná plocha $\kappa^{\ast}$ je rovina kolmá k oběma osám
Příklad 2: Sestrojte průnikovou křivku rotačních ploch $\kappa$ (osa $o$, hlavní polomeridián $m$)
a $\kappa'$ (osa $o'$, hlavní polomeridián $m'$).
a $\kappa'$ (osa $o'$, hlavní polomeridián $m'$).
Osy různoběžné
Pomocná plocha $\kappa^{\ast}$ je kulová plocha se středem v průsečíku os
Další materiály:
Příklad 3 a 4
Sestrojte průnikovou křivku rotačních ploch $\kappa$ (osa $o$, hlavní polomeridián $m$)
a $\kappa'$ (osa $o'$, hlavní polomeridián $m'$).
a $\kappa'$ (osa $o'$, hlavní polomeridián $m'$).
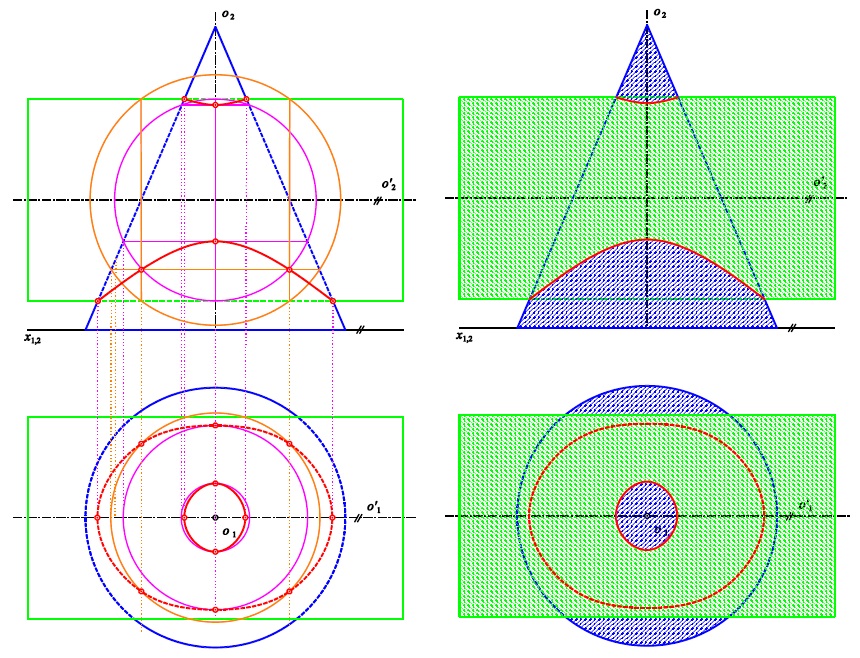
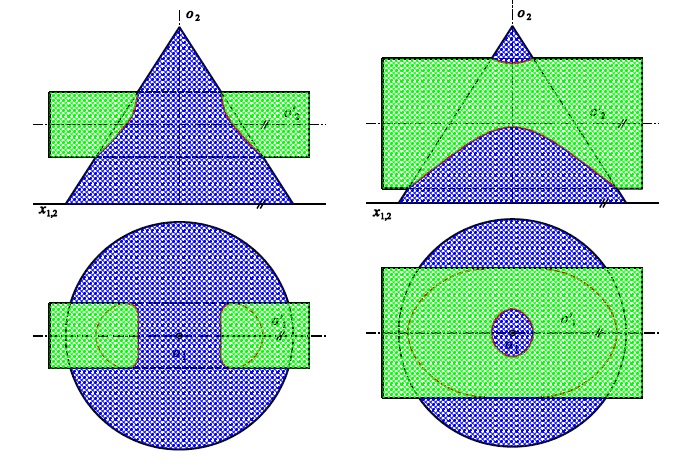
Průniku kužele válcem nebo válce kuželem?
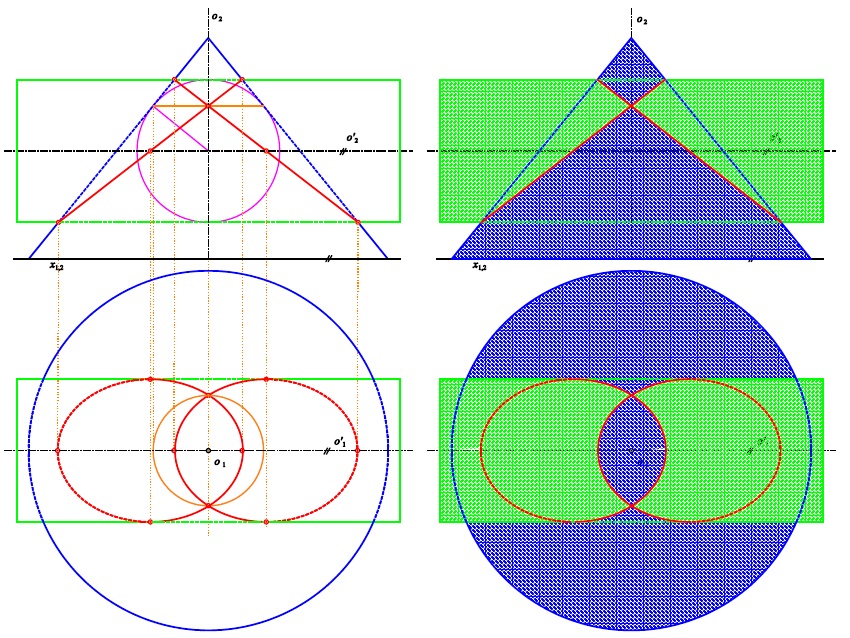
Rozpad průniku dvou rotačních kvadratických ploch
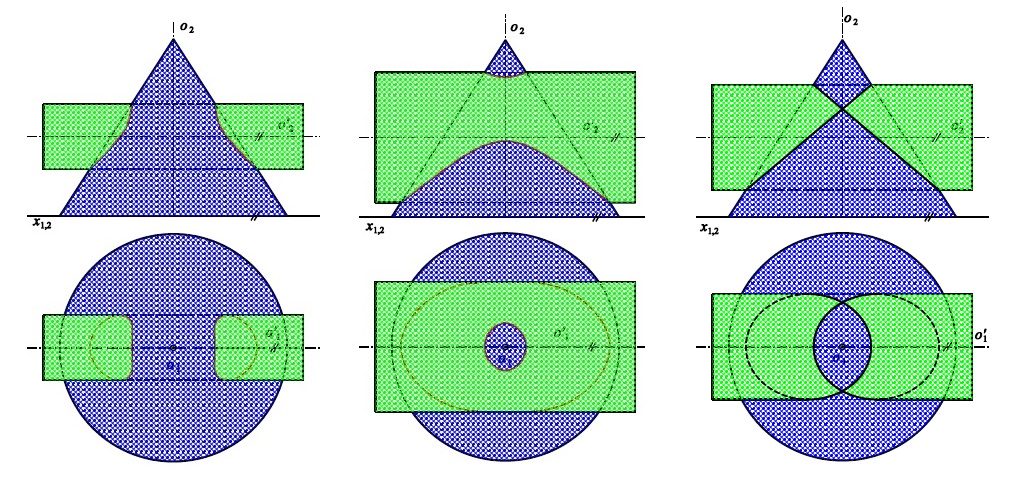
Pokud lze oběma rotačním kvadrikám vepsat společnou kulovou plochu se středem v průsečíku os, pak se jejich průnik rozpadá na dvě kuželosečky.
V případě rotačních válcových a kuželových ploch se průnik rozpadne na dvě elipsy.

příště: