Konstruktivní geometrie 2023/24
Rotační plochy
Rotační plocha
vzniká rotací křivky $k$ ( tvořící křivka ) kolem přímky $o$ ( osa rotace).
(Např. rotací kuželosečky kolem její osy vznikne rotační kvadratická plocha.)
(Např. rotací kuželosečky kolem její osy vznikne rotační kvadratická plocha.)
- určení rotační plochy: tvořící křivka $k$, osa rotace $o$
- každý bod při rotaci opisuje kružnici (v rovině kolmé k ose, střed na ose)
→ rovnoběžková kružnice

Výběr zobrazovací metody
Úmluva: osa rotace kolmá k půdorysně
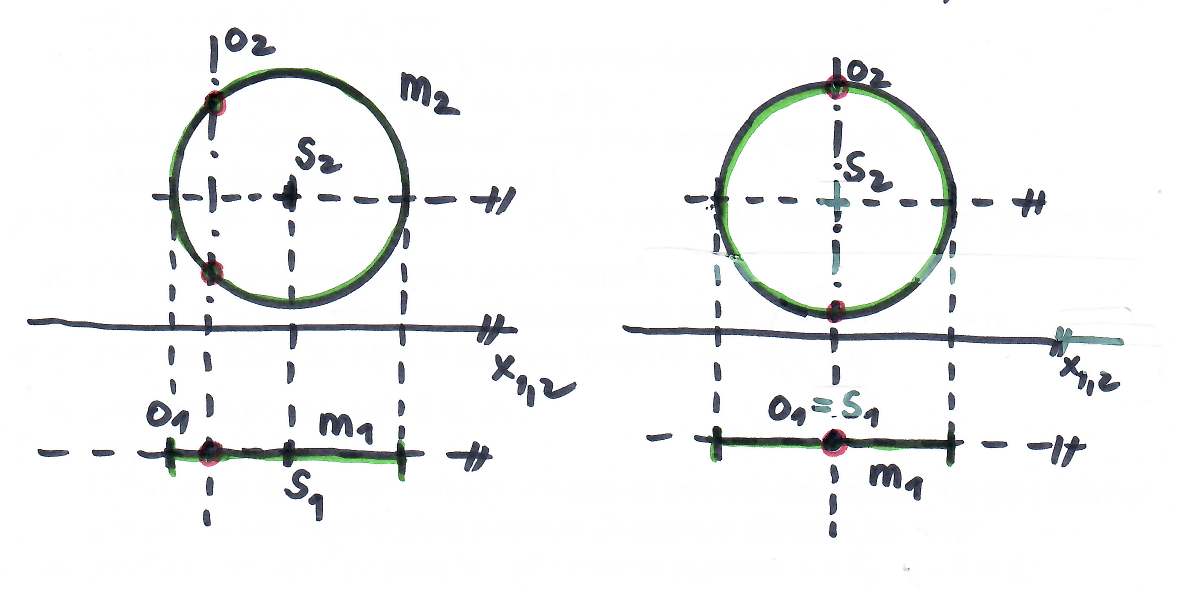
Základní úloha - rovnoběžková kružnice
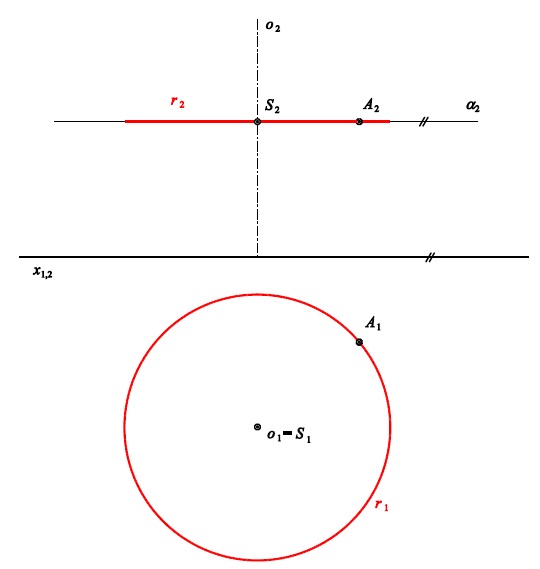
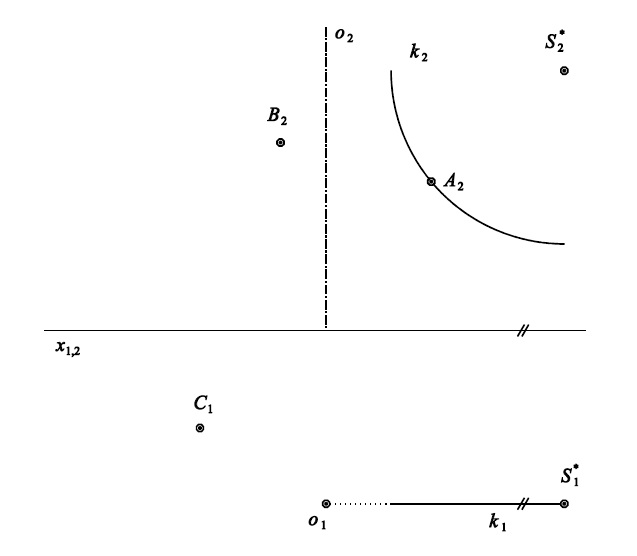
Př.1: Zobrazte rovnoběžkovou kružnici $r$, která vznikne rotací bodu $A$ kolem osy $o$.
Zadání rotační plochy
Tvořicí křivka:
- spojitá, bez uzlových bodů, po částech hladká
- obecně prostorová

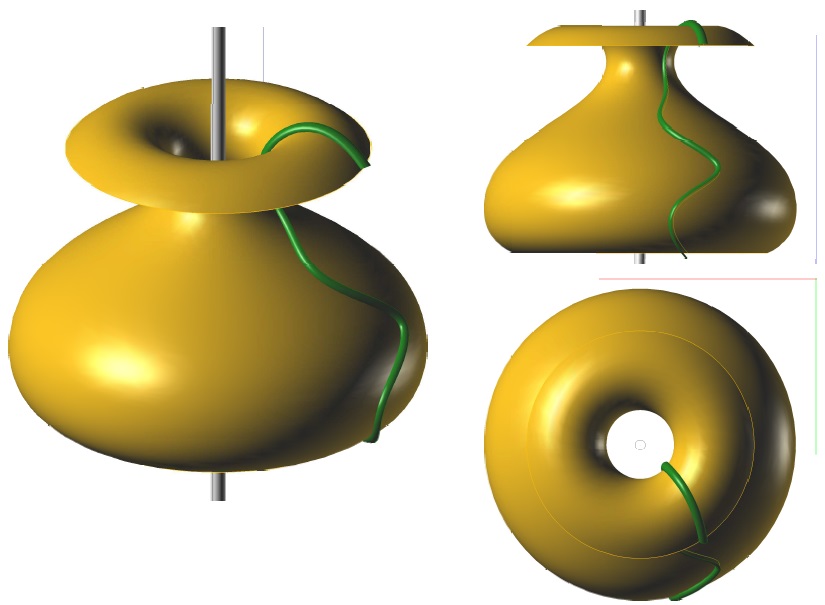
Pokud tvořicí křivka leží v rovině procházející osou rotace
- pak se jedná o tzv. polomeridián,
polomeridián spolu se svým osově souměrným obrazem tvoří meridián rotační plochy
- pak se jedná o tzv. polomeridián,
polomeridián spolu se svým osově souměrným obrazem tvoří meridián rotační plochy

Křivka meridiánu (polomeridiánu) se tedy dá určit jako osový řez obecně dané rotační plochy
Pokud je navíc meridián (polomeridián) v rovině rovnoběžné s nárysnou
- pak je to tzv. hlavní meridián (polomeridián)
- pak je to tzv. hlavní meridián (polomeridián)

Hlavní meridián (polomeridián) je tedy osový řez plochy rovinou rovnoběžnou s nárysnou.
Příklady rotačních ploch
Rotační plochy přímkové
tvořicí křivka $k$ je přímka
- různoběžná s osou → kuželová plocha (rotační)
- rovnoběžná s osou → válcová plocha (rotační)
- mimoběžná s osou → jednodílný hyperboloid (rotační)
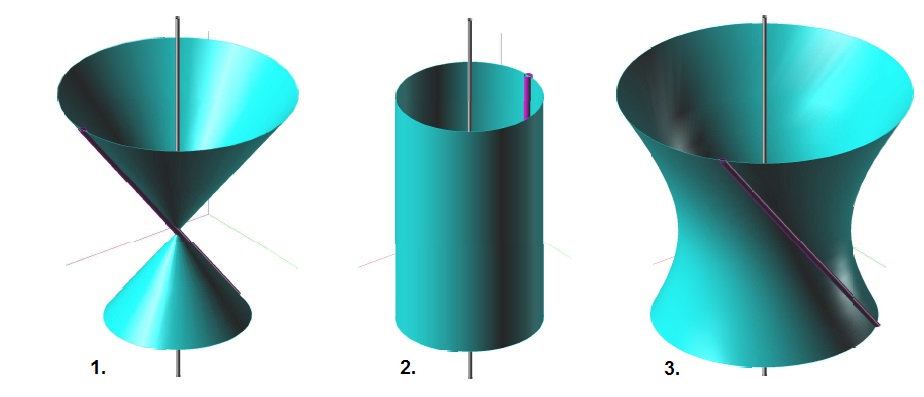
Rotační kuželová plocha
zadání v Mongeově promítání
Rotační válcová plocha
zadání v Mongeově promítání
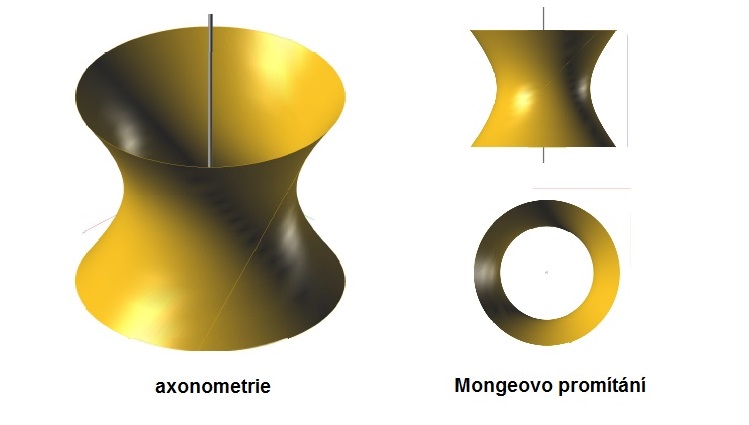
Jednodílný rotační hyperboloid
Jednodílný rotační hyperboloid
zadání v Mongeově promítání
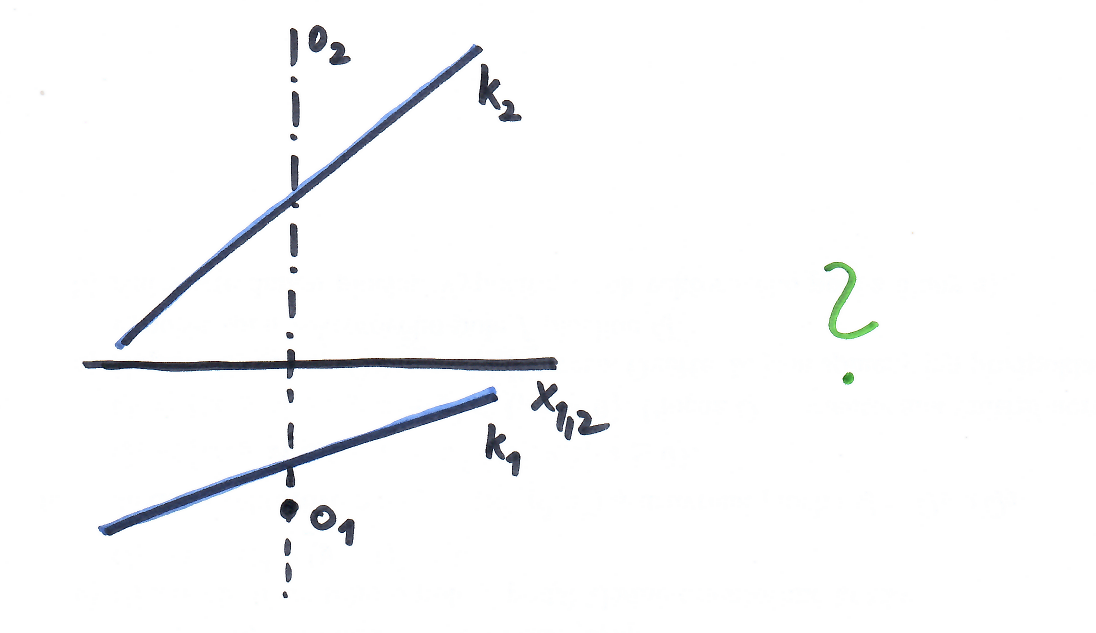
Rotační přímkové plochy
Rotační plochy cyklické
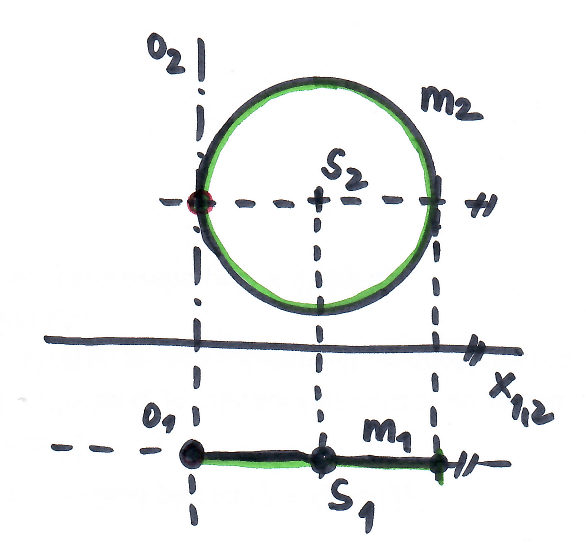
tvořicí kružnice $k$ je polomeridián
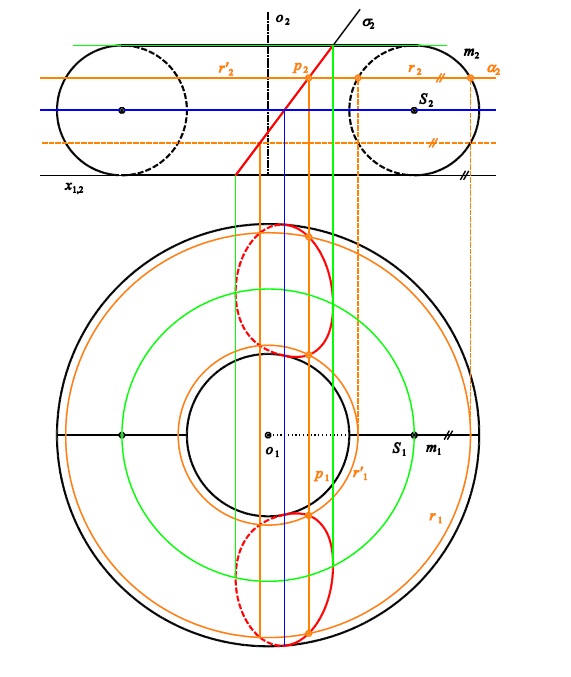
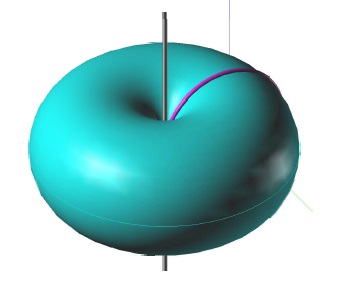
- kružnice neprotíná osu rotace → anuloid (toroid)

Zadání anuloidu v Mongeově promítání
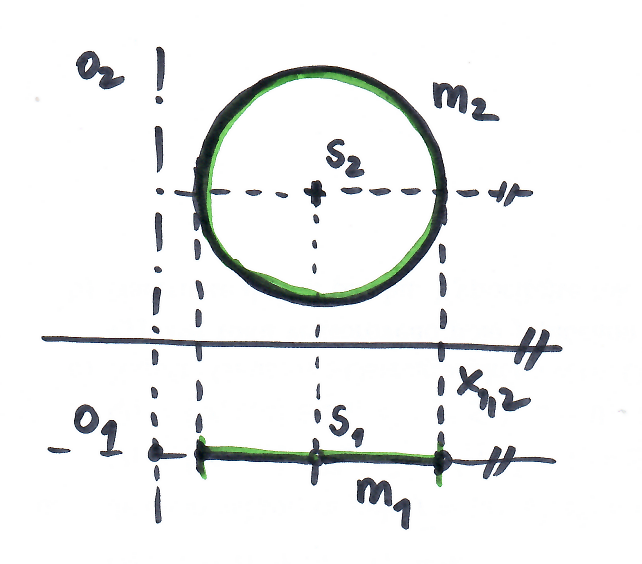
Rotační plochy cyklické - méně známé (*)
tvořicí kružnice $k$ je polomeridián
- kružnice se dotýká osy rotace → axoid
Zadání axoidu v Mongeově promítání
Rotační plochy cyklické - méně známé (*)
tvořicí kružnice $k$ je polomeridián
- kružnice protíná osu rotace ve dvou bodech → melanoid
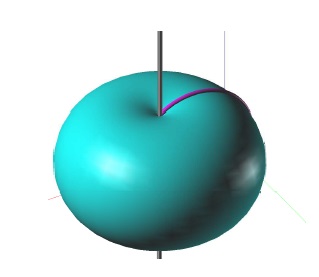
Zadání melanoidu v Mongeově promítání
Tečná rovina a normála
Tečná rovina $\tau$ v bodě $A$ rotační plochy ($k, o$)
- rovina tvořená tečnami ke všem křivkám na ploše, které prochází daným bodem $A$,
k určení stačí najít 2 různoběžné
určení tečné roviny v bodě tvořicí křivky:
tečna k rovnoběžkové kružnici + tečna k tvořící křivce
tečna k rovnoběžkové kružnici + tečna k tvořící křivce
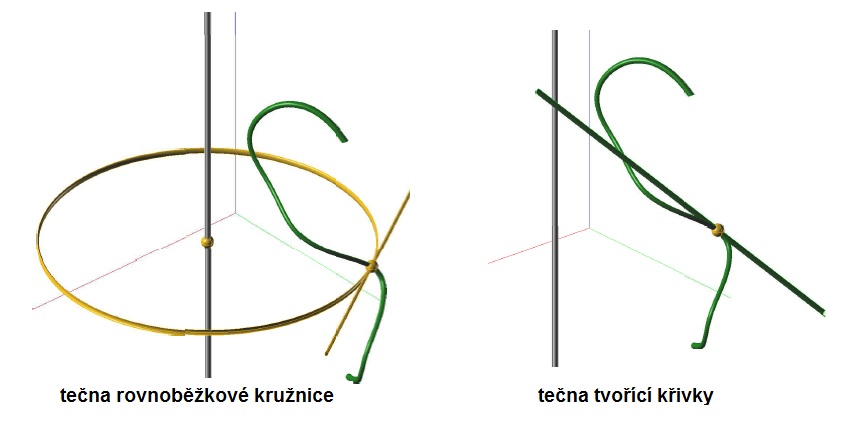
Normála $n$ rotační plochy ($k, o$) v bodě $A$
- normála $n$ je kolmice k tečné rovině $\tau$
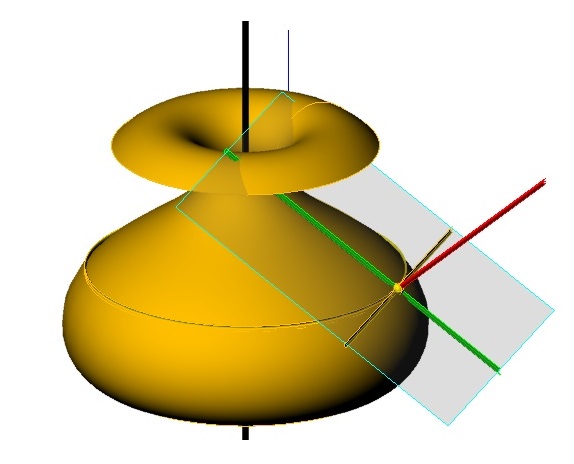
Normála rotační plochy - vlastnosti
- normály sestrojené ve všech bodech jedné obecné rovnoběžkové kružnice vytvoří kuželovou plochu s vrcholem na ose rotace
(ve speciálních případech pak válcovou plochu nebo rovinu)
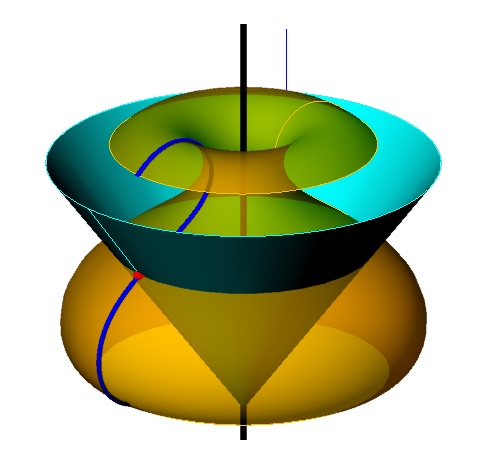
- normála v bodě polomeridiánu je normálou křivky polomeridiánu
Základní úloha - tečná rovina
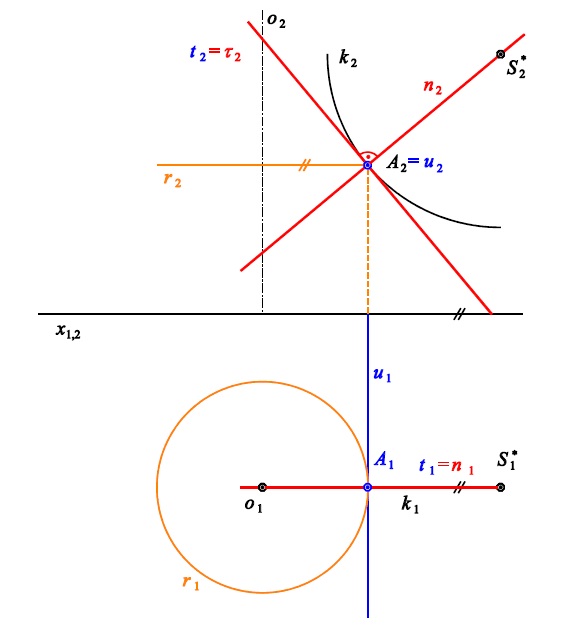
Př. 2: Rotační plocha je určena osou rotace $o$ a křivkou $k$.
V bodě $A$ plochy určete tečnou rovinu $\tau$ a normálu $n$ plochy.
V bodě $A$ plochy určete tečnou rovinu $\tau$ a normálu $n$ plochy.
Tečná rovina v bodě hlavního meridiánu
- tečna k rovnoběžkové kružnici je kolmá k nárysně
- tečná rovina je kolmá k nárysně
- nárysem tečné roviny je tečna k nárysu křivky hlavního meridiánu
pomůcka: průmět tečny ke křivce = tečna k průmětu křivky
Normála v bodě hlavního meridiánu
- je kolmá k tečné rovině (tečná rovina kolmá k nárysně)
- je rovnoběžná s nárysnou
- je normálou hlavního meridiánu!
výsledek:

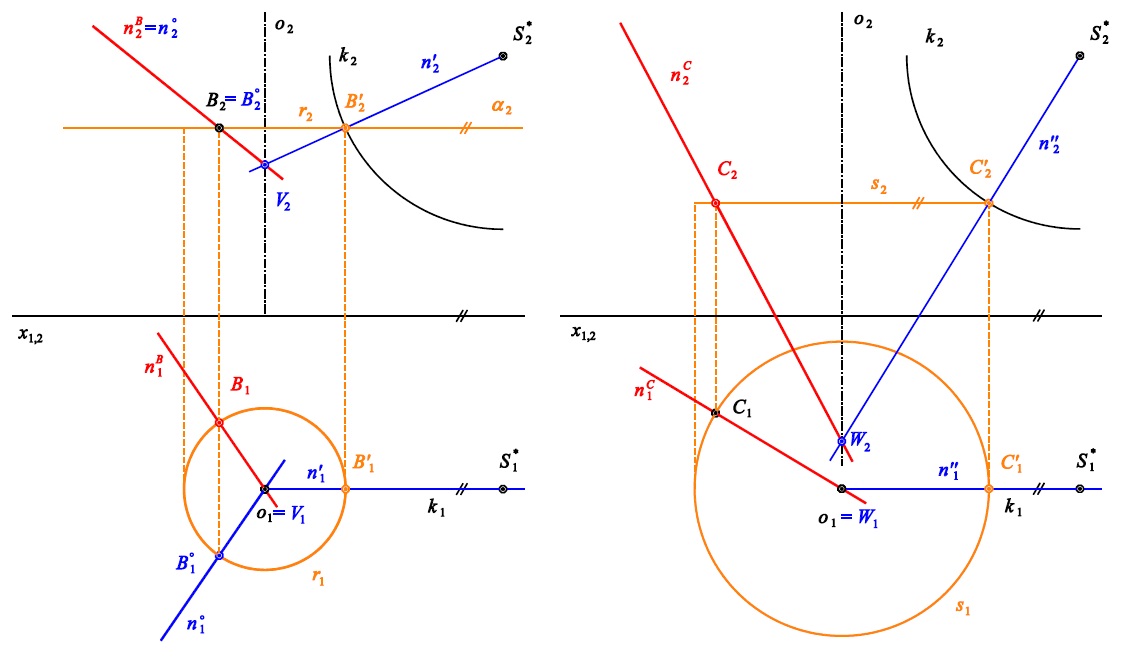
Základní úloha
- bod plochy, normála
Př. 3 + 4: Sestrojte normálu $n$ rotační plochy v bodě $B$ a $n´$ v bodě $C$ plochy.

výsledek:

Průměty rotační plochy v Mongeově promítání
Významné rovnoběžkové kružnice
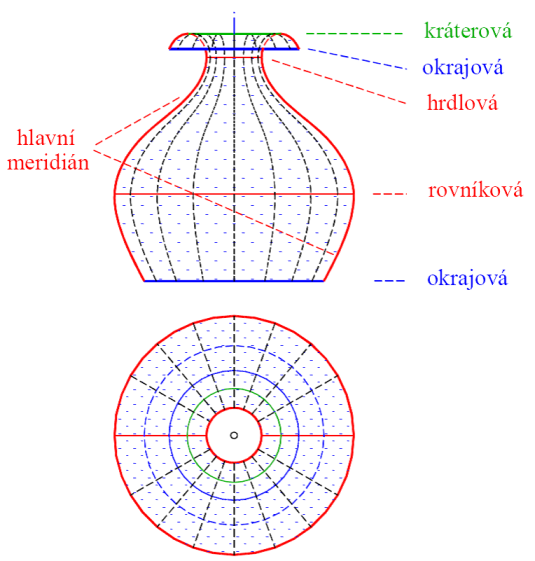
Průměty rotační plochy
- půdorys tvoří rovnoběžkové kružnice okrajové, hrdlové, rovníkové
- nárys je složen z křivek hlavního meridiánu a nárysů okrajových a kráterových rovnoběžkových kružnic
Základní úloha - průměty
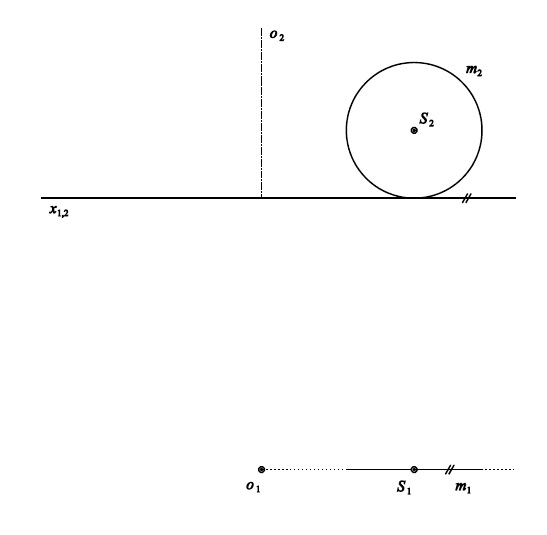
Př. 6: Zobrazte oba průměty plochy dané hlavním polomeridiánem $m$ a osou rotace $o$.
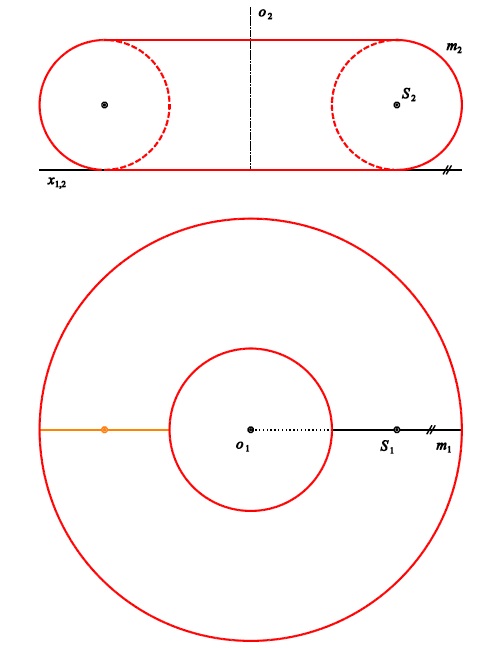
výsledek:

Řezy rotačních ploch
Řezy pouze rovinami ve speciální poloze
- rovina řezu kolmá k půdorysně (např. osový řez)
- rovina řezu kolmá k nárysně
Obecný postup bodové konstrukce řezu:
- pomocná rovina $\alpha$ kolmá k ose rotace
- rovnoběžková kružnice $r$ v rovině $\alpha$
- průsečnice $p$ roviny řezu a roviny $\alpha$
- průsečíky kružnice $r$ a přímky $p$
- volba další roviny $\alpha$ ...
Základní úloha
- řez rovinou kolmou k půdorysně
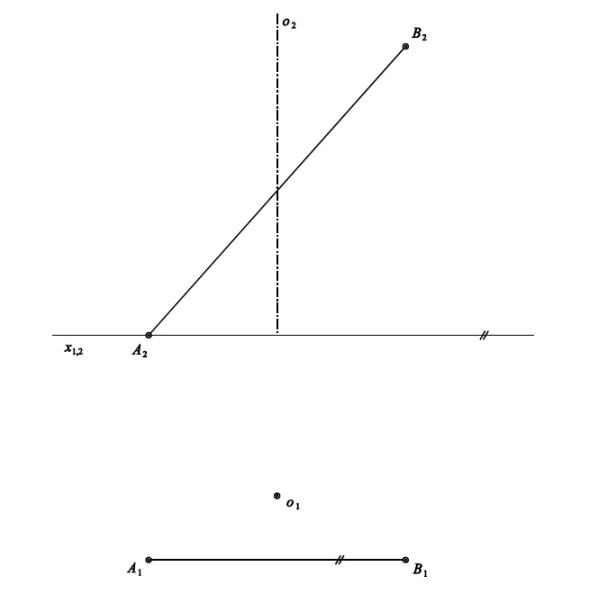
Př. 5: Rotační plocha je určena osou rotace $o$ a tvořící úsečkou $AB$. Zobrazte oba průměty plochy.
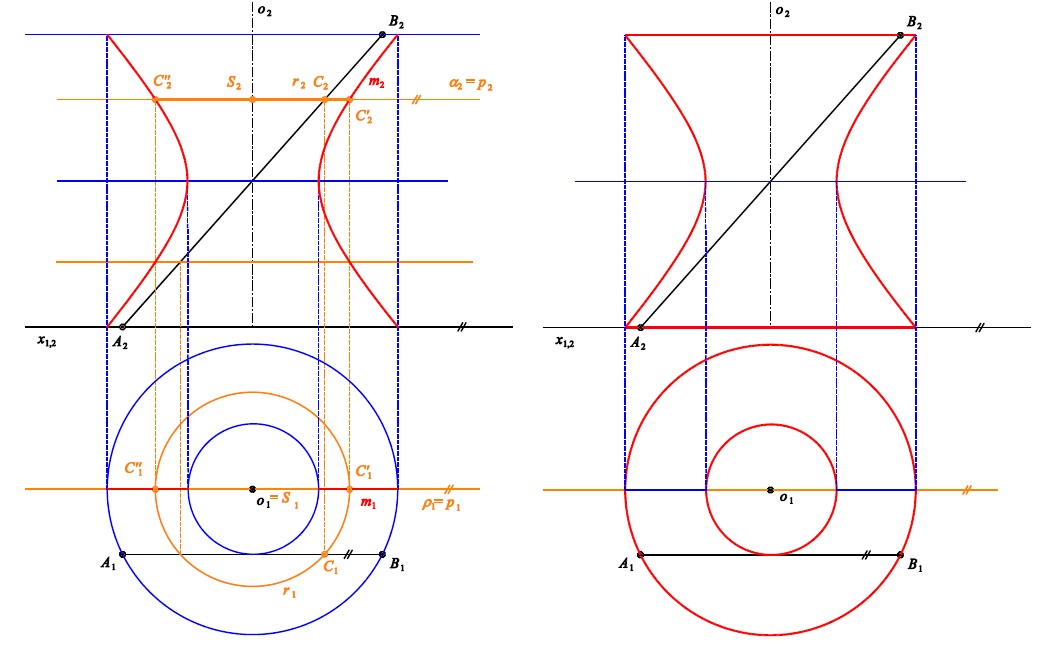
Základní úloha
- řez rovinou kolmou k nárysně
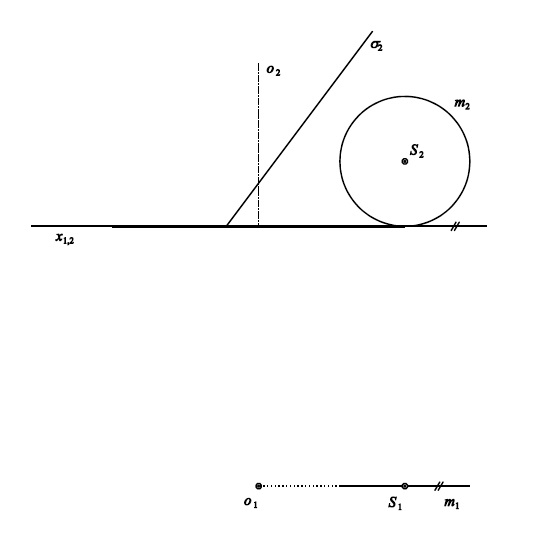
Jak vypadá řešení úlohy v prostoru?