Konstruktivní geometrie 2023/24

Kvadratické plochy

Kvadratická plocha

  • zkráceně kvadrika
  • plocha vyjádřená implicitně rovnicí druhého stupně
  • obecný tvar: \[\alpha x^2+\beta y^2 + \gamma z^2 + \delta xy + \eta xz + \theta yz + \kappa x + \lambda y + \mu z + \nu = 0\]

    • pokud jsou osy kvadriky rovnoběžné s osami $x,y,z$: \[\alpha x^2+\beta y^2 + \gamma z^2 +\kappa x + \lambda y + \mu z + \nu = 0\]

    • kanonický tvar: \[\frac{(x-m)^i}{a}+\frac{(y-n)^j}{b}+\frac{(z-p)^k}{c}=d,\]
      \[a,b,c\in\mathbb{R}-\{0\},d\in\{0,1\}, i,j,k\in \{0,1,2\}\]

    • kvadrika v základní poloze $\Leftrightarrow$ střed nebo vrchol kvadriky v bodě $[m, n, p]=[0,0,0]$
    • kvadrika v posunuté poloze $\Leftrightarrow$ střed nebo vrchol v bodě $[m, n, p]\neq[0,0,0]$
  • další studijní materiál
Př.1: Najděte kanonický tvar rovnice kvadratické plochy \[2x^2-8x+3y^2+18y+6z+29=0\] a zjistěte, o jakou plochu se jedná.
úpravy (postupně)

$2x^2-8x+3y^2+18y+6z+29=0$
$2(x^2-4x)+3(y^2+6y)+6z+29=0$
$2(x-2)^2+3(y+3)^2+6z+29=0+8+27$
$2(x-2)^2+3(y+3)^2+6z-6=0$
$2(x-2)^2+3(y+3)^2+6(z-1)=0/:6$

kanonický tvar:

\[\frac{(x-2)^2}{3}+\frac{(y+3)^2}{2}+(z-1)=0\]
$[2,-3,1]$ je významný bod (střed nebo vrchol) kvadriky
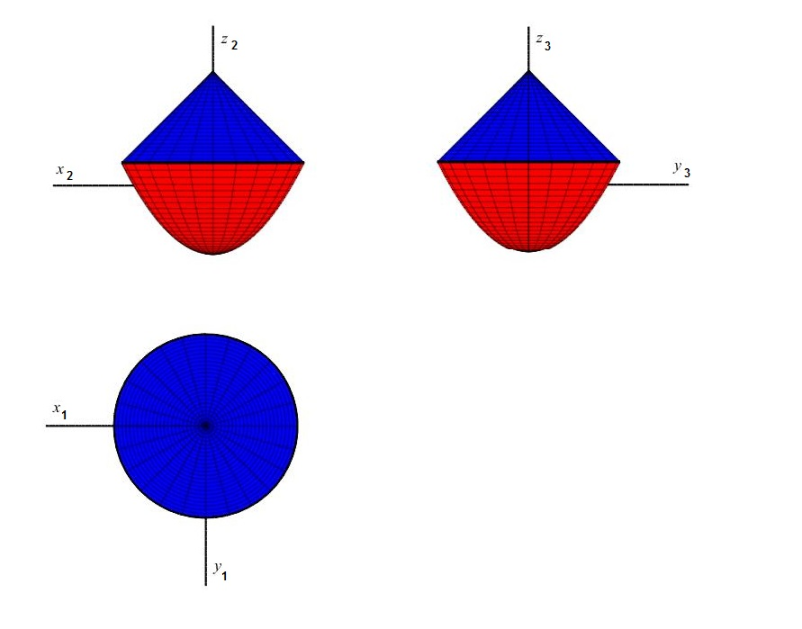
Typ kvadriky určit z řezových křivek hlavními rovinami (nejlépe významným bodem)
řez hlavní rovinou rovnoběžnou s půdorysnou $\pi$, tj. s rovinou os $x,y$

\[z=1 \implies \frac{(x-2)^2}{3}+\frac{(y+3)^2}{2}=0\]
bod v rovině $z=1$, $[2,-3,1]$

$z>1 \implies \frac{(x-2)^2}{3}+\frac{(y+3)^2}{2}=-(z-1) \implies$ žádný bod
$z<1 \implies \frac{(x-2)^2}{3}+\frac{(y+3)^2}{2}=-(z-1) \implies$ elipsa
řez hlavní rovinou rovnoběžnou s nárysnou $\nu$, tj. s rovinou os $x,z$

\[y=-3 \implies \frac{(x-2)^2}{3}+(z-1)=0\]
parabola v rovině $y=-3$, $V=[2,-3,1]$
řez hlavní rovinou rovnoběžnou s bokorysnou $\mu$, tj. s rovinou os $y,z$

\[x=2 \implies \frac{(y+3)^2}{2}+(z-1)=0\]
jiná parabola v rovině $x=2$, $V=[2,-3,1]$
\[\frac{(x-2)^2}{3}+\frac{(y+3)^2}{2}+(z-1)=0\]
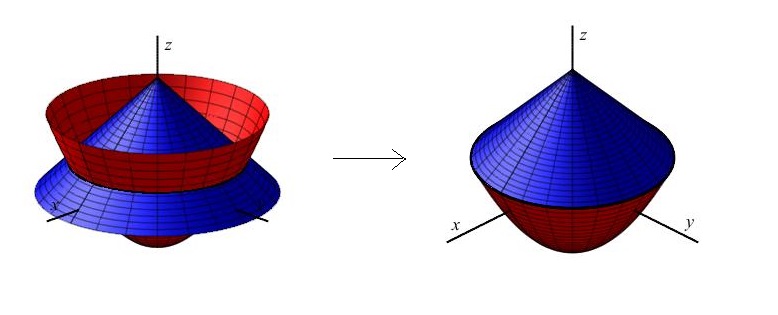
eliptický paraboloid

charakteristiky:
vrchol $V=[2,-3,1]$, osa $o: X(t)=V+t(0,0,1); t\in\mathbb{R}$, orientace $-$

Určení typu kvadriky (+ úvodní teorie)

klasifikace obecných kvadrik

podle kanonického tvaru rovnice
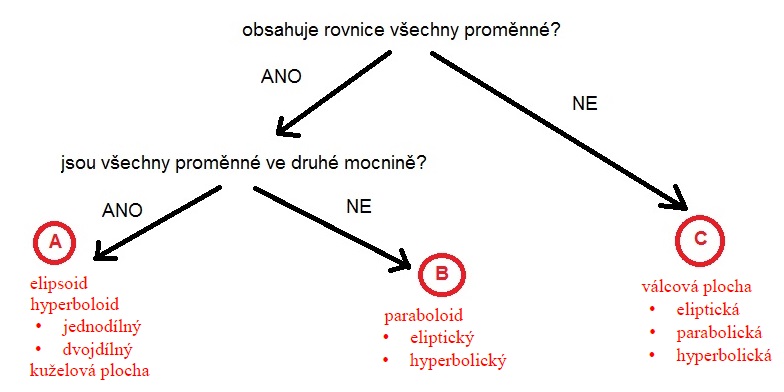
skupina A (elipsoid, hyperboloidy, kuželová plocha)
Obecný elipsoid (tříosý)
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{b^2}\color{red}{+}\frac{z^2}{c^2}=\color{red}{1}\]
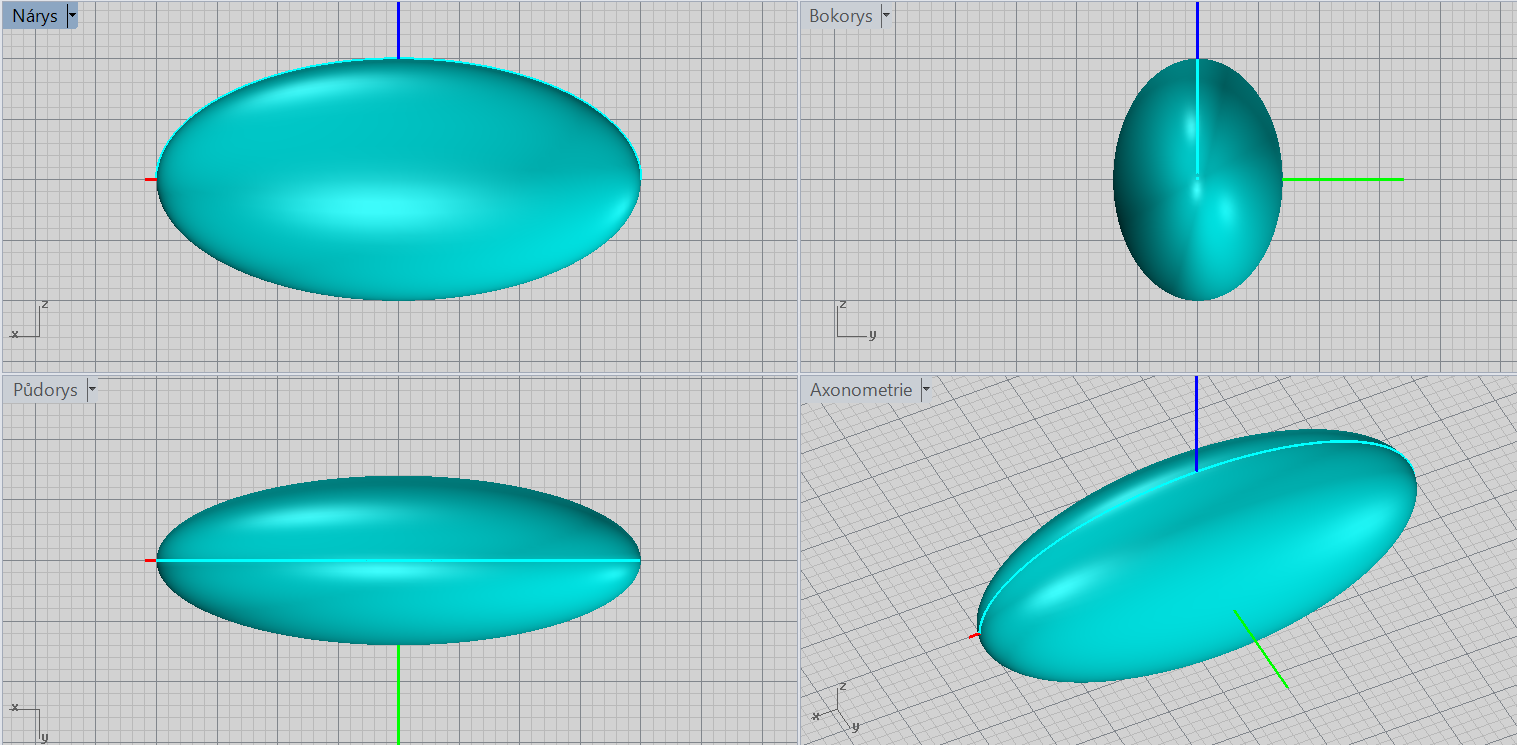
Charakteristiky: střed, velikosti poloos
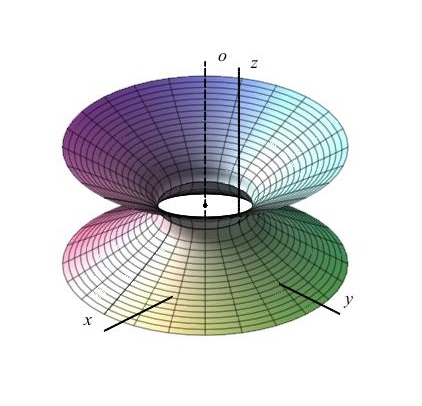
Jednodílný eliptický hyperboloid
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{b^2}\color{red}{-}\frac{z^2}{c^2}=\color{red}{1}\]
Charakteristiky: střed, hlavní osa (znaménko - v rovnici)
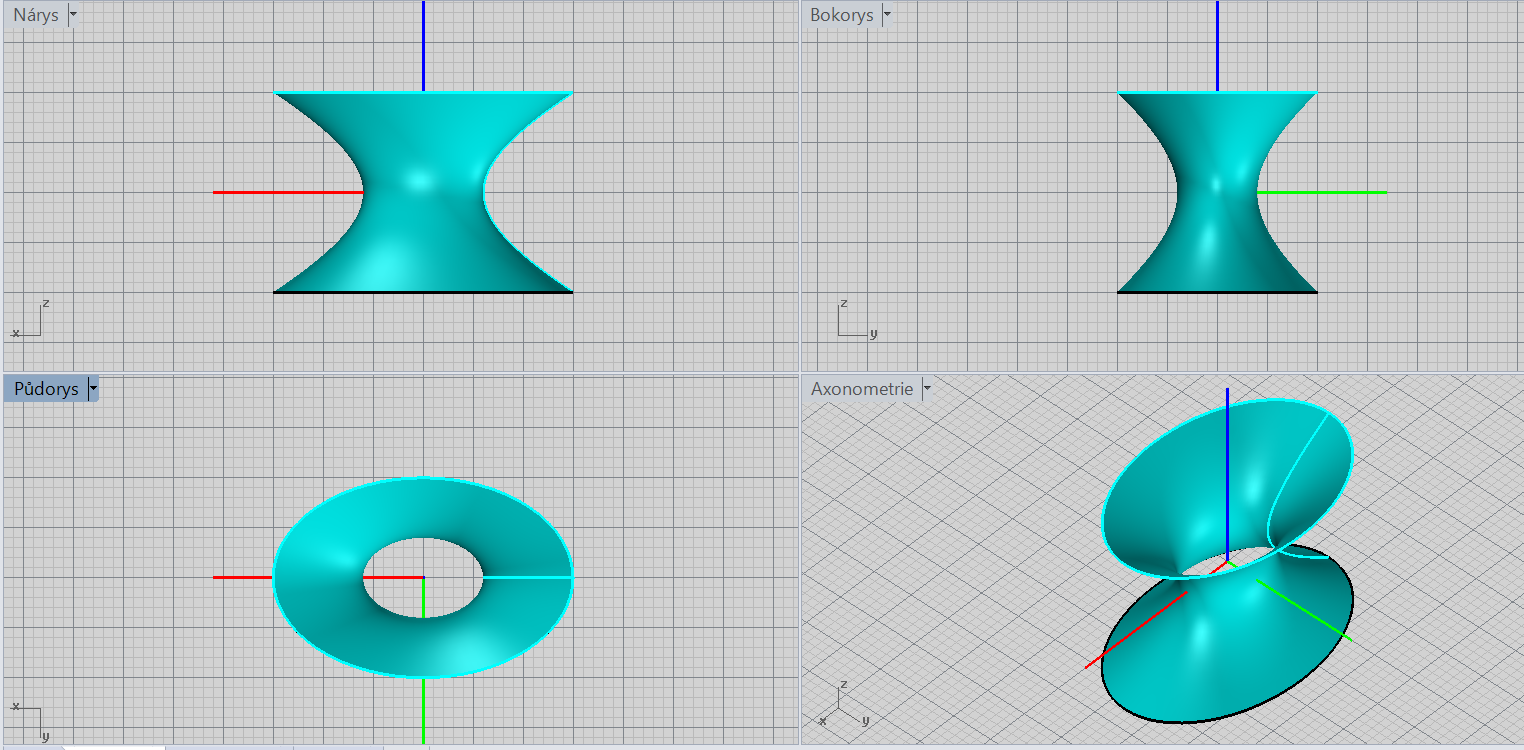
Dvojdílný eliptický hyperboloid
\[\color{red}{-}\frac{x^2}{a^2}\color{red}{-}\frac{y^2}{b^2}\color{red}{+}\frac{z^2}{c^2}=\color{red}{1}\]
Charakteristiky: střed, hlavní osa ("rušivé" znaménko v rovnici), vrcholy
Eliptická kuželová plocha
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{b^2}\color{red}{-}\frac{z^2}{c^2}=\color{red}{0}\]
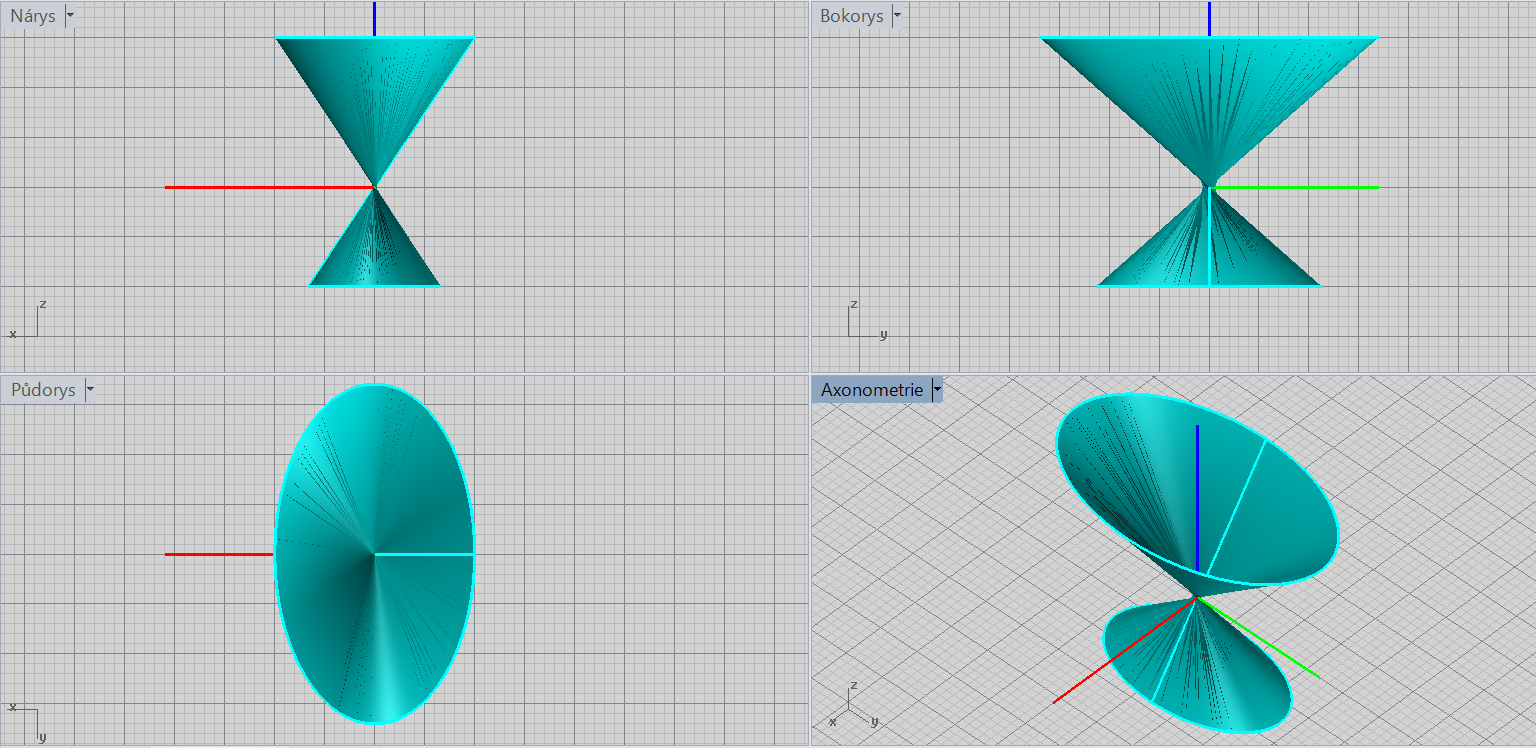
Charakteristiky: vrchol, osa ("rušivé" znaménko v rovnici)
skupina B (paraboloidy)
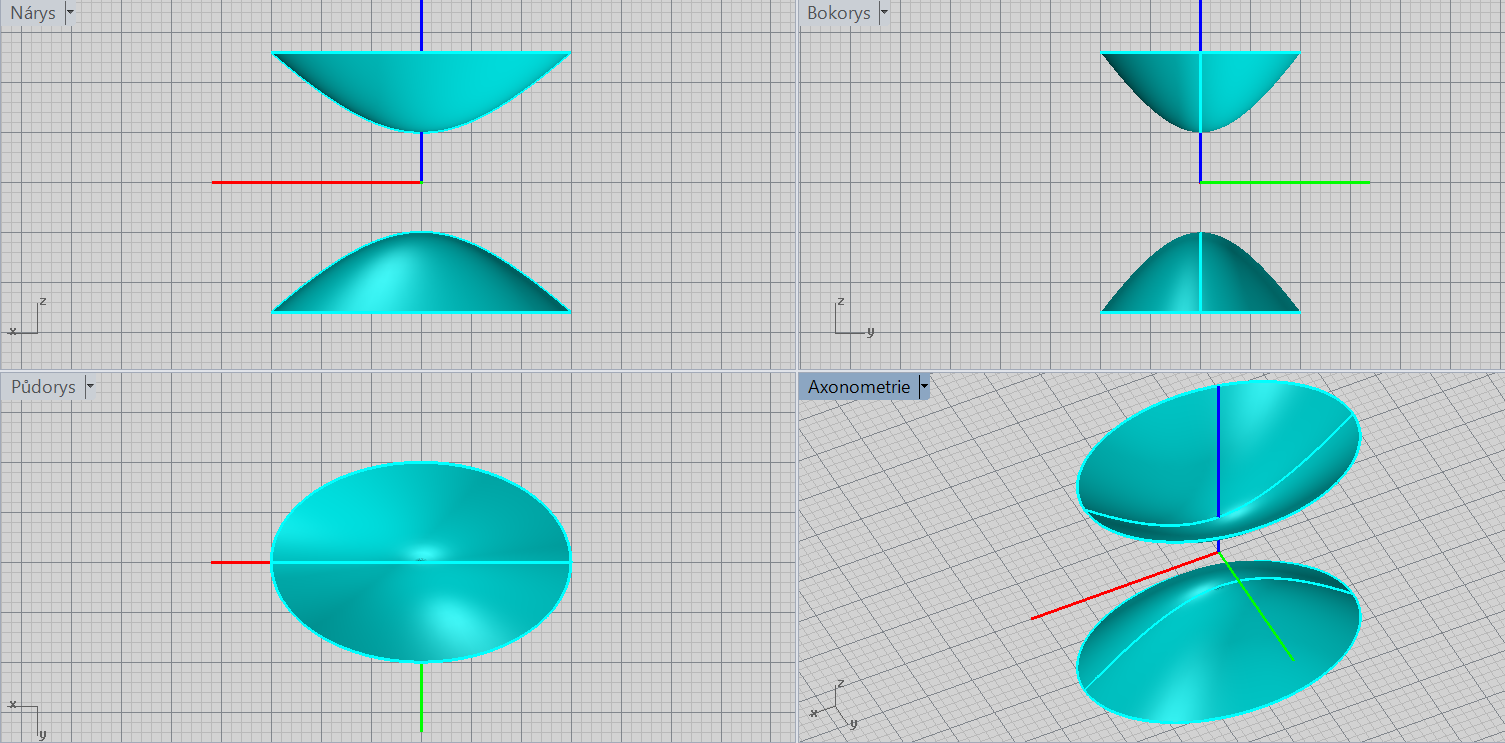
Eliptický paraboloid
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{b^2}\color{red}{\pm}z=\color{red}{0}\]
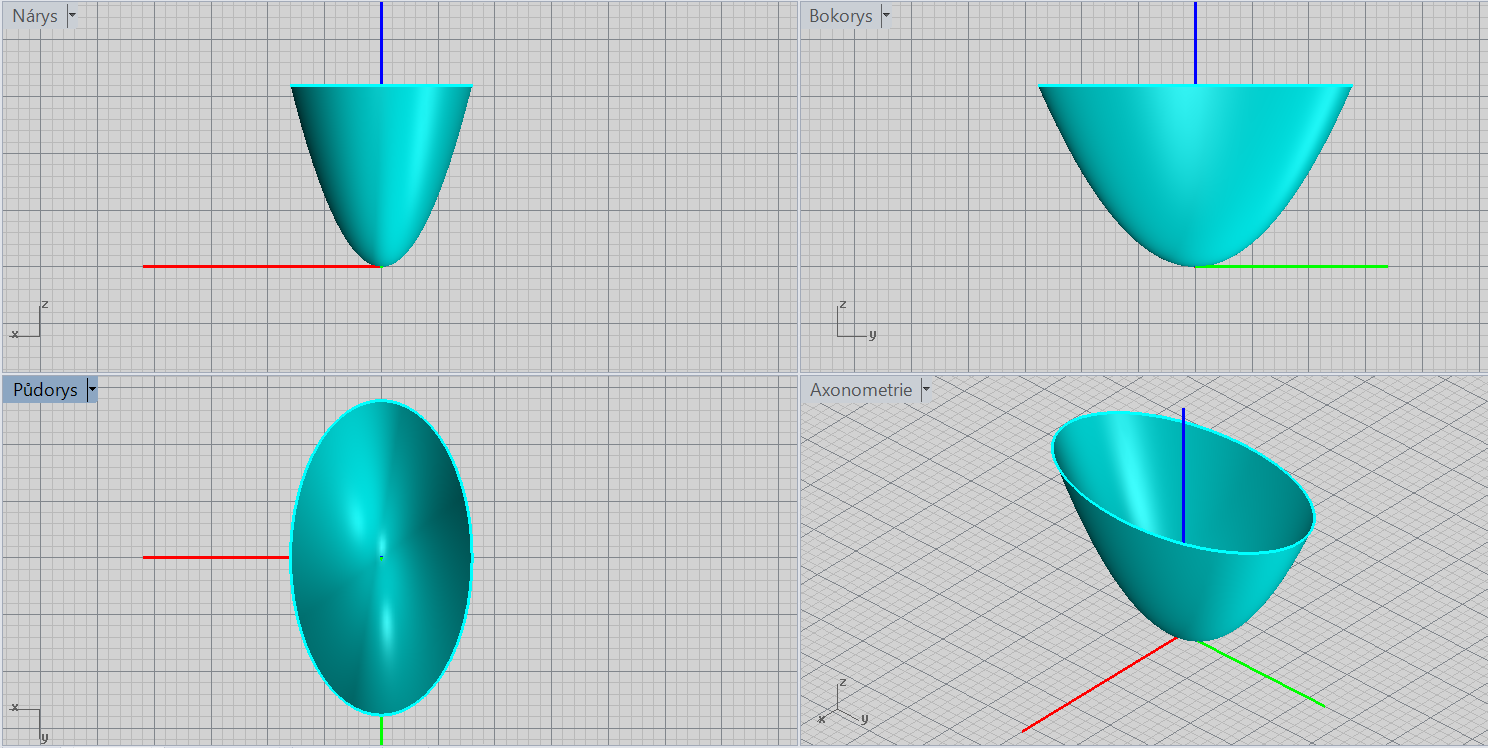
Charakteristiky: vrchol, osa (podle lineárního členu), orientace
Hyperbolický paraboloid
Hyperbolický paraboloid
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{-}\frac{y^2}{b^2}\color{red}{\pm}z=\color{red}{0}\]
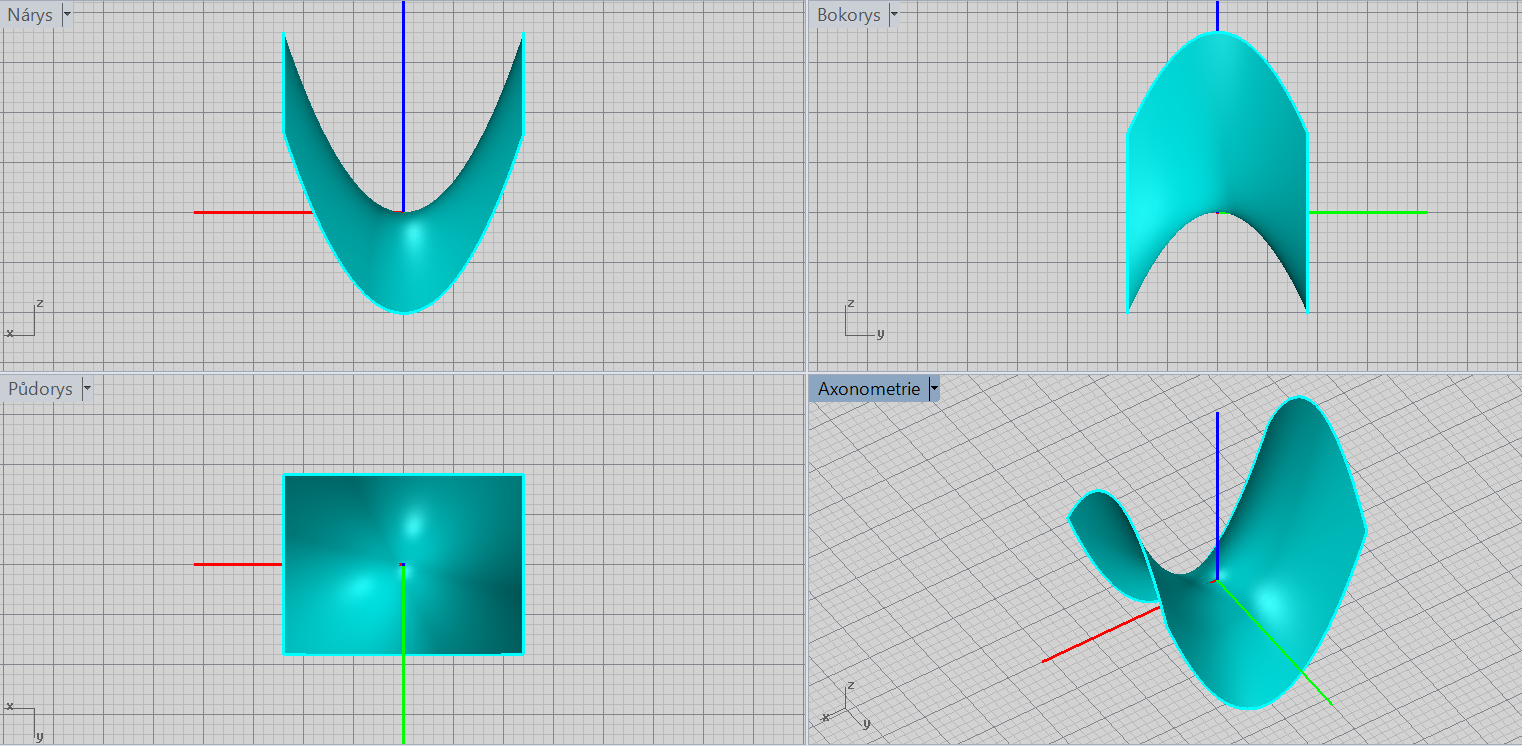
Charakteristiky: sedlový bod, osa (podle lineárního členu)
Hyperbolický paraboloid
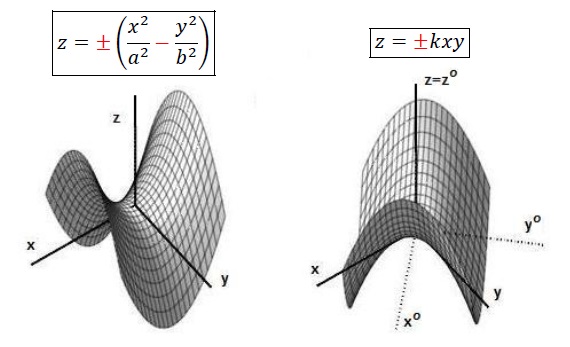
skupina C (válcové plochy)
Eliptická válcová plocha
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{b^2}=\color{red}{1}\]
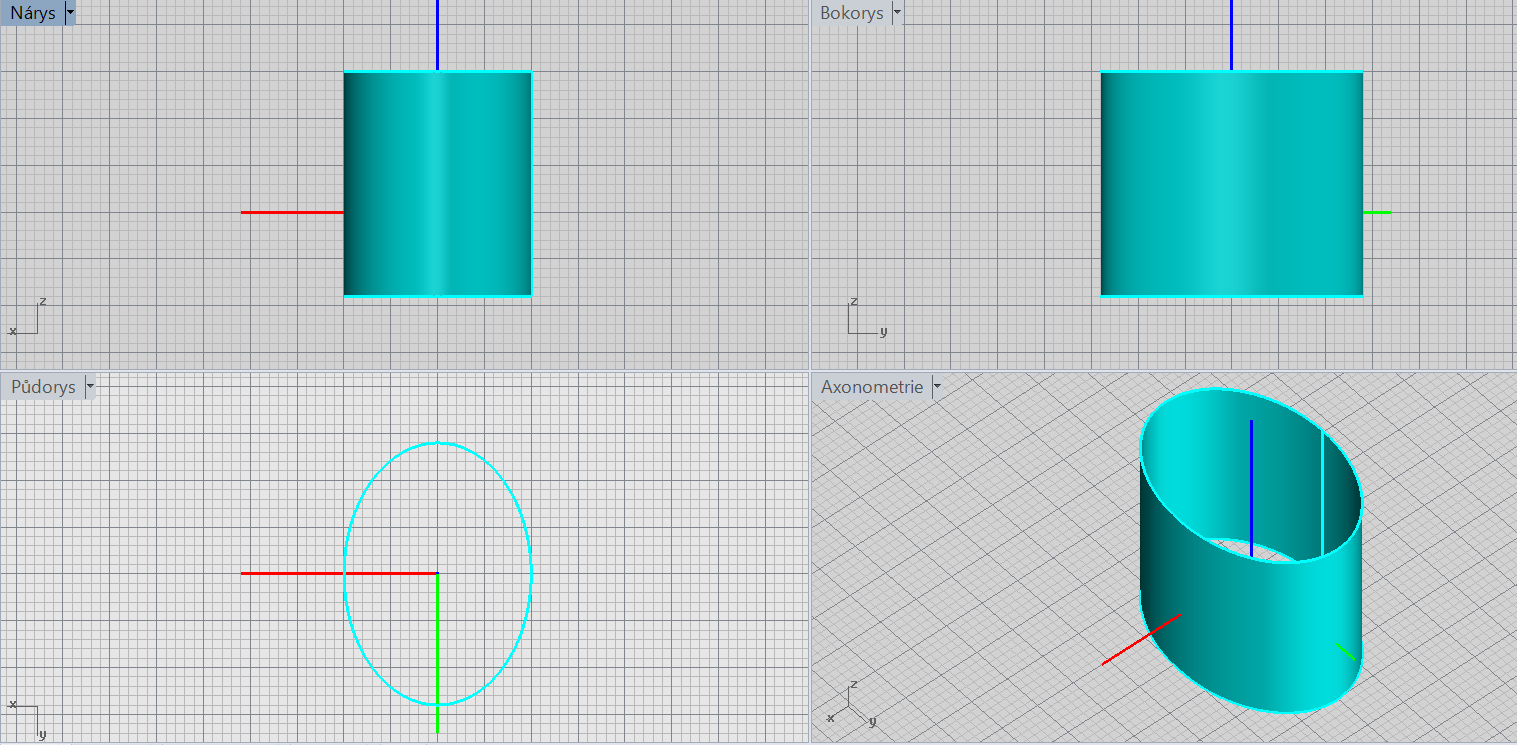
Charakteristiky: tvořicí křivka, osa (chybějící proměnná)
Hyperbolická válcová plocha
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{-}\frac{y^2}{b^2}=\color{red}{\pm 1}\]
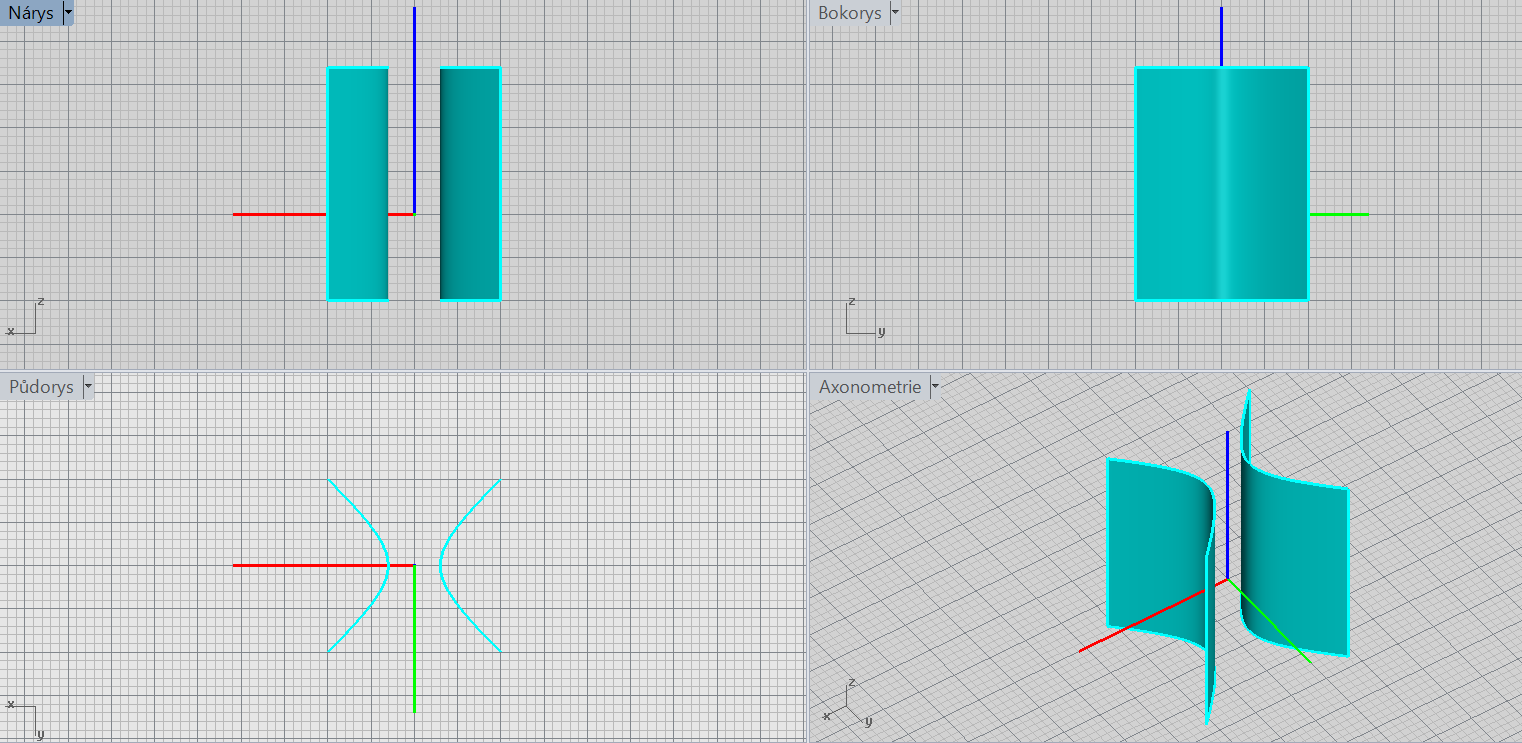
Charakteristiky: tvořicí křivka, osa (chybějící proměnná)
Parabolická válcová plocha
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{\pm}y=\color{red}{0}\]
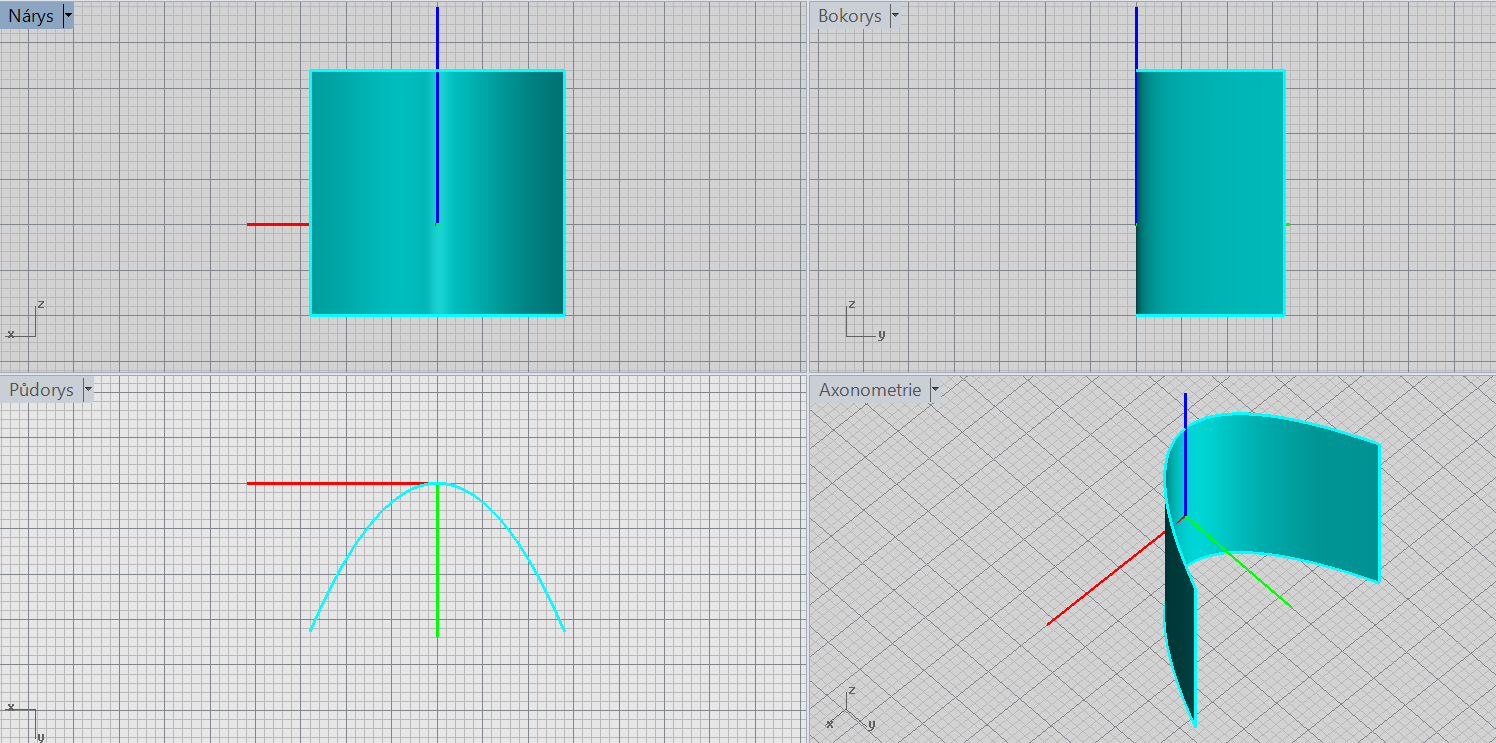
Charakteristiky: tvořicí křivka, osa (chybějící proměnná)

Rotační kvadratická plocha

\[\alpha x^2+\beta y^2 + \gamma z^2 + \kappa x + \lambda y + \mu z + \nu =0\]

rotační $\Leftrightarrow (\alpha=\beta) \lor (\beta=\gamma)\lor(\alpha=\gamma)$

rotační $\Leftrightarrow$ stejný koeficient u kvadratických členů (včetně znaménka!)

Princip vytvoření rotačních kvadrik
jako rotačních ploch

rotací kuželosečky kolem její osy souměrnosti
elipsa $\frac{x^2}{a^2}+\frac{z^2}{c^2}=1 \implies$ rotační elipsoid $\frac{x^2}{a^2}+\frac{y^2}{a^2}+\frac{z^2}{c^2}=1$
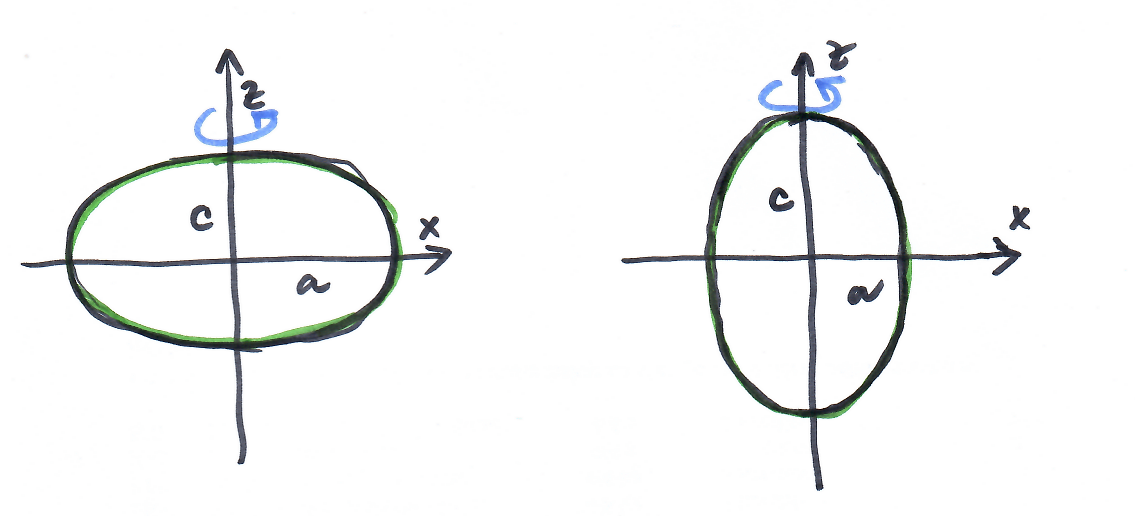
hyperbola $\frac{x^2}{a^2}-\frac{z^2}{c^2}=1 \implies$ rotační hyperboloid $\frac{x^2}{a^2}+\frac{y^2}{a^2}-\frac{z^2}{c^2}=1$
hyperbola $-\frac{x^2}{a^2}+\frac{z^2}{c^2}=1 \implies$ rotační hyperboloid $-\frac{x^2}{a^2}-\frac{y^2}{a^2}+\frac{z^2}{c^2}=1$
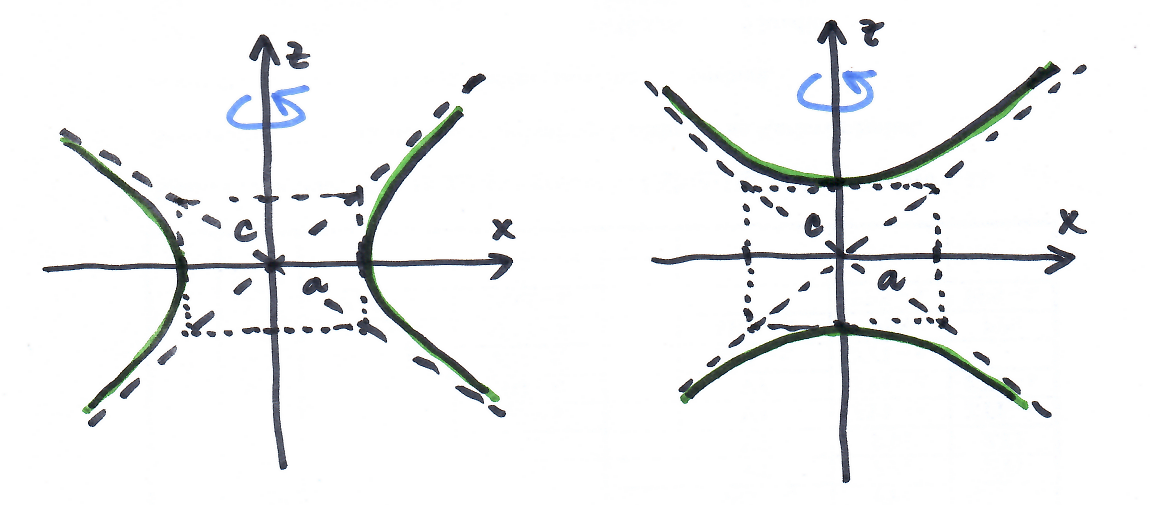
parabola $\frac{x^2}{a^2}-z=0 \implies$ rotační paraboloid $\frac{x^2}{a^2}+\frac{y^2}{a^2}-z=0$
parabola $\frac{x^2}{a^2}+z=0 \implies$ rotační paraboloid $\frac{x^2}{a^2}+\frac{y^2}{a^2}+z=0$
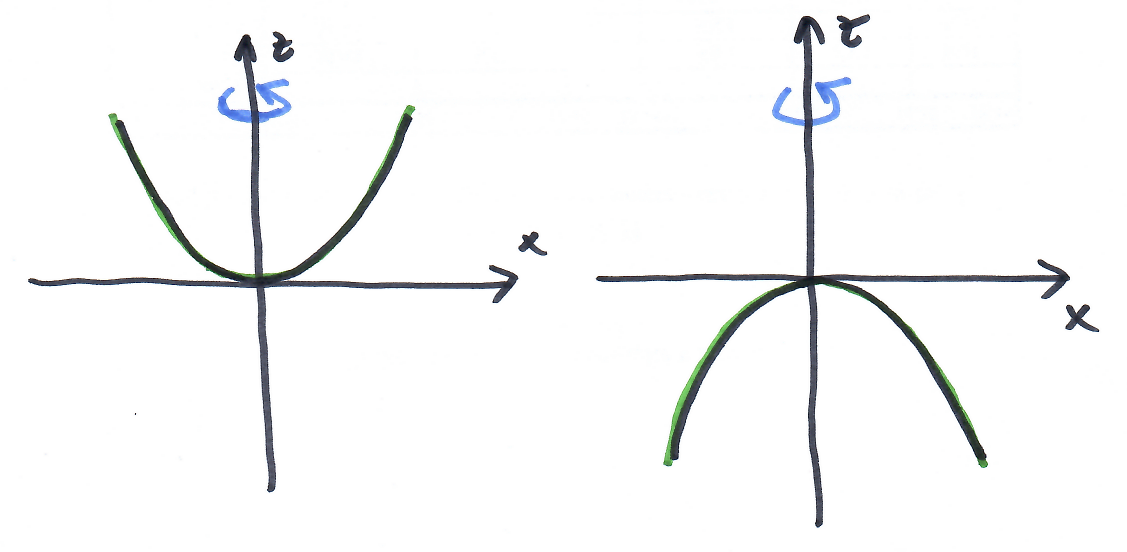
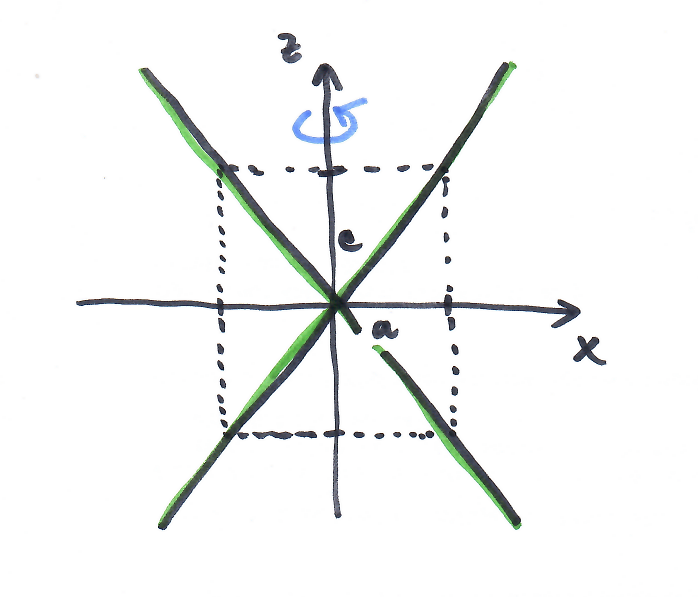
dvojice různoběžek $\frac{x^2}{a^2}-\frac{z^2}{c^2}=0 \implies$ rotační kuželová plocha $\frac{x^2}{a^2}+\frac{y^2}{a^2}-\frac{z^2}{c^2}=0$
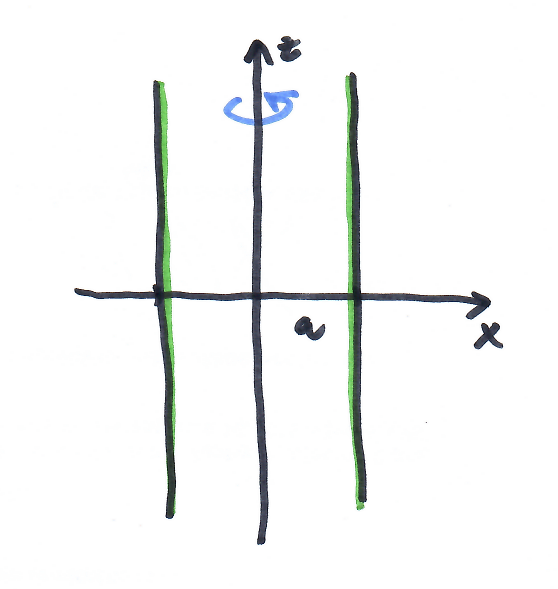
dvojice rovnoběžek $\frac{x^2}{a^2}=1 \implies$ rotační válcová plocha $\frac{x^2}{a^2}+\frac{y^2}{a^2}=1$

klasifikace rotačních kvadrik

podle kanonického tvaru rovnice
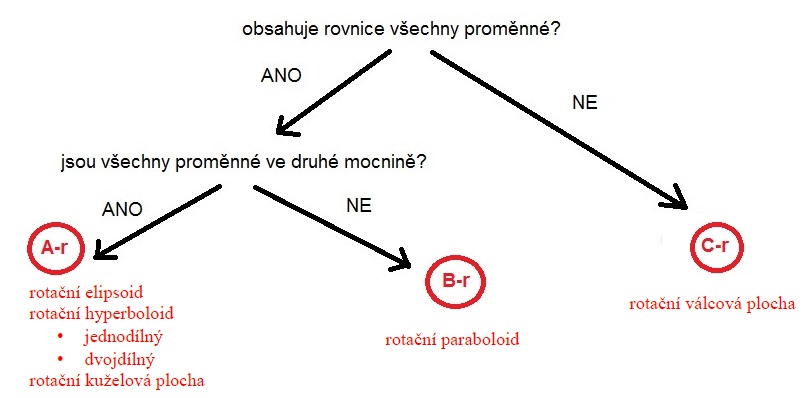
skupina A-r (elipsoid, hyperboloidy, kuželová plocha)
Rotační elipsoid
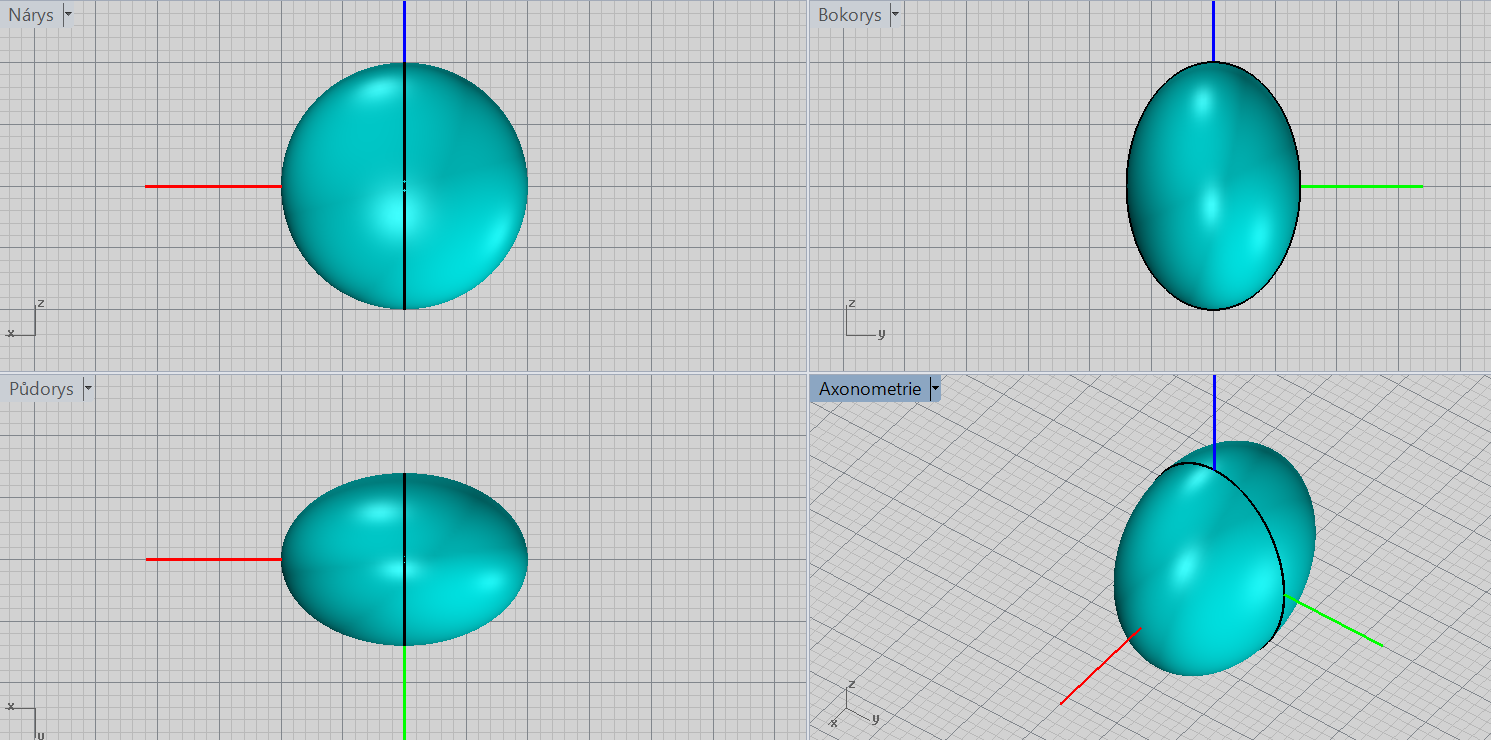
Rotační elipsoid - protáhlý
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{a^2}\color{red}{+}\frac{z^2}{c^2}=\color{red}{1};\ a< c\]
Charakteristiky: střed, poloosy, osa rotace
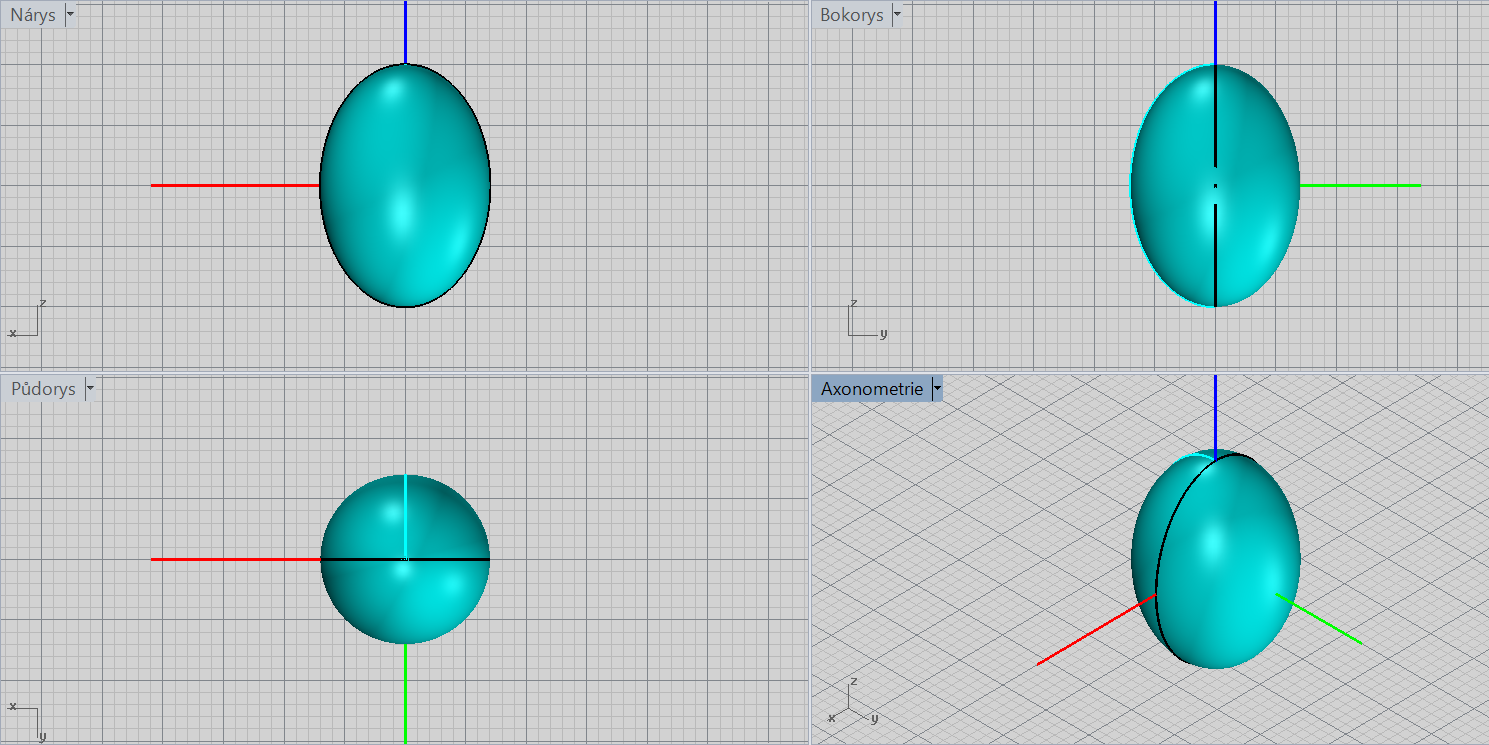
Rotační elipsoid - protáhlý
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{b^2}\color{red}{+}\frac{z^2}{b^2}=\color{red}{1};\ a> b\]
Charakteristiky: střed, poloosy, osa rotace
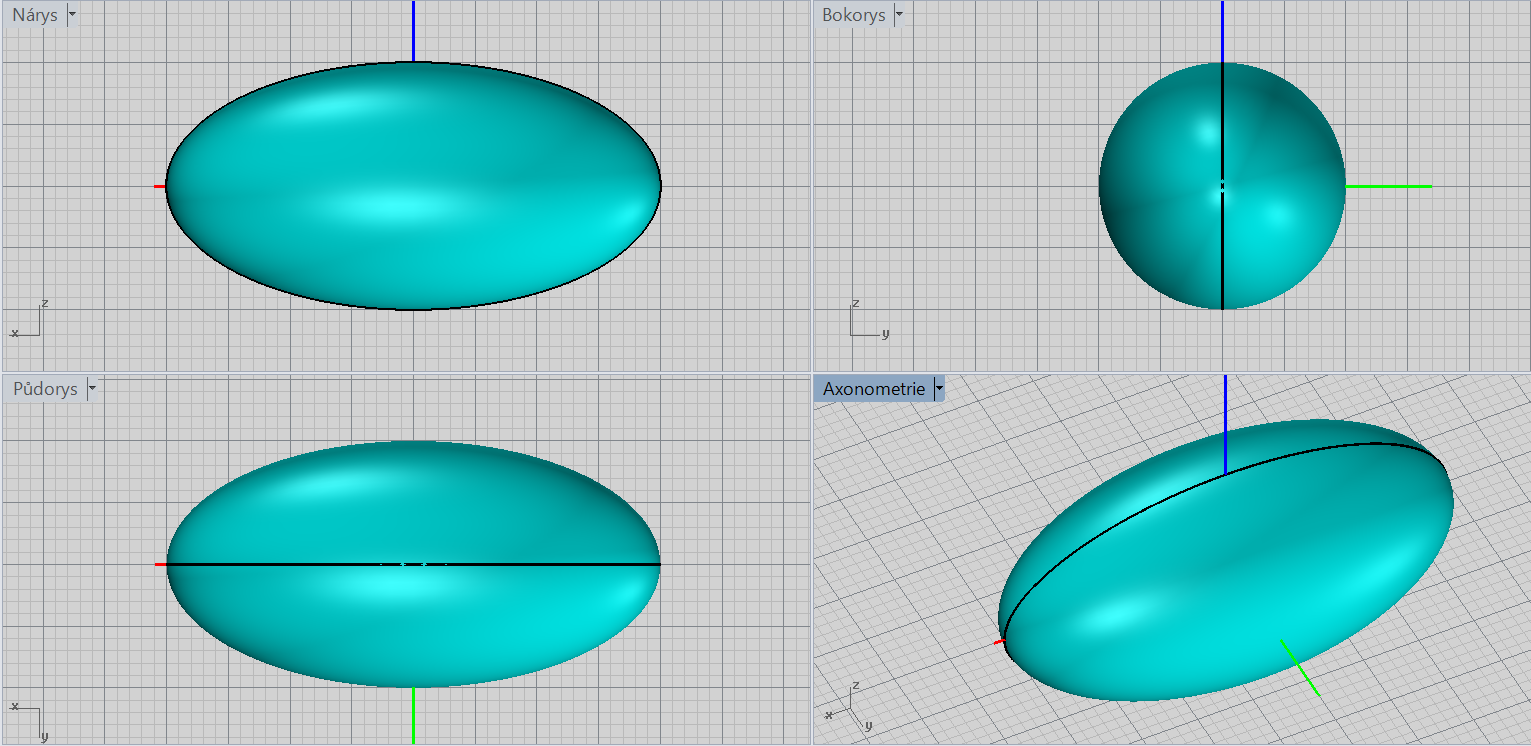
Rotační elipsoid - zploštělý
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{a^2}\color{red}{+}\frac{z^2}{c^2}=\color{red}{1};\ a> c \]
Charakteristiky: střed, poloosy, osa rotace
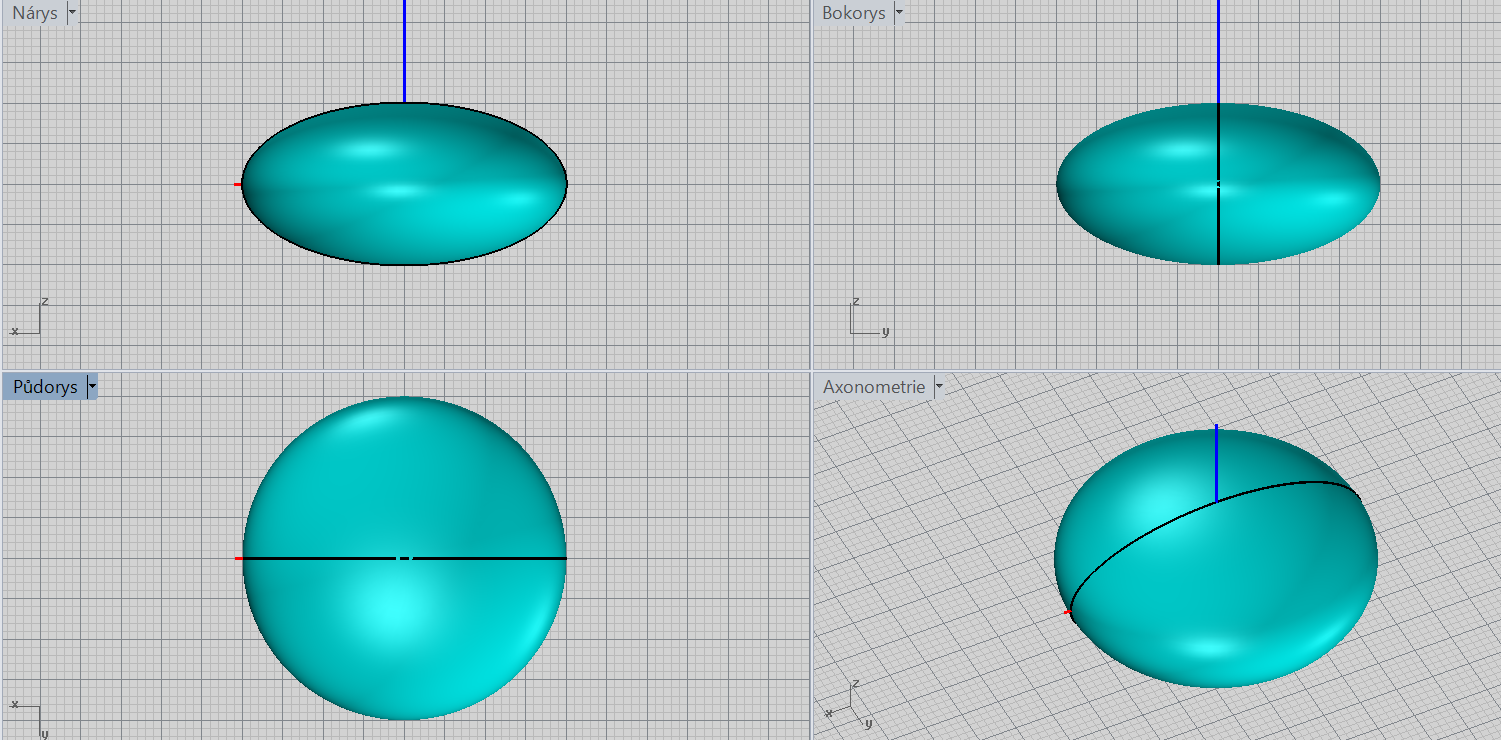
Rotační elipsoid - zploštělý
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{b^2}\color{red}{+}\frac{z^2}{a^2}=\color{red}{1};\ a> b \]
Charakteristiky: střed, poloosy, osa rotace
rotační elipsoid
speciální rotační elipsoid - kulová plocha
Rotační hyperboloid - jednodílný
Rotační hyperboloid - jednodílný
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{a^2}\color{red}{-}\frac{z^2}{c^2}=\color{red}{1}\]
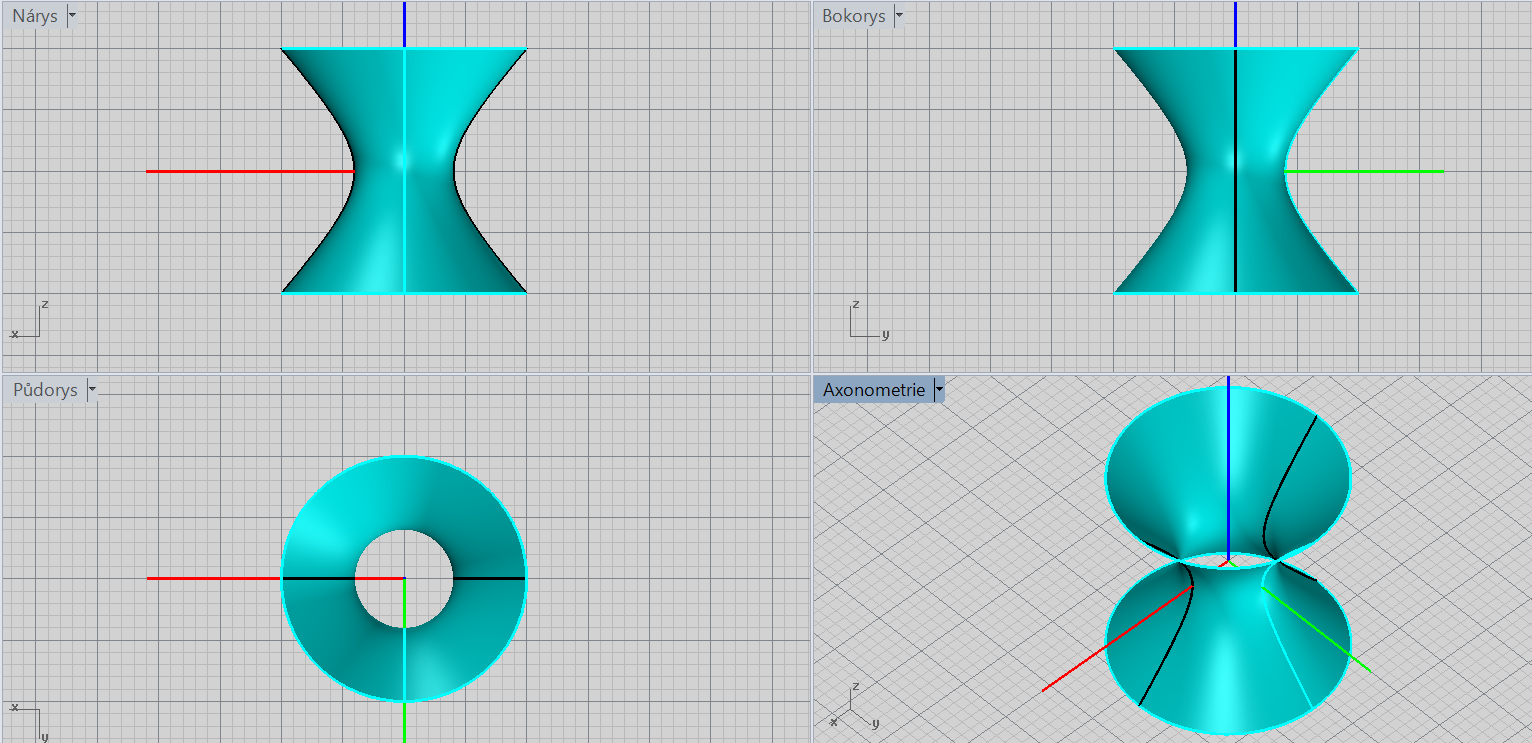
Charakteristiky: střed, osa rotace
Rotační hyperboloid - dvojdílný
\[\color{red}{-}\frac{x^2}{a^2}\color{red}{-}\frac{y^2}{a^2}\color{red}{+}\frac{z^2}{c^2}=\color{red}{1} \]
Charakteristiky: střed, vrcholy, osa rotace
Rotační kuželová plocha
Rotační kuželová plocha
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{a^2}\color{red}{-}\frac{z^2}{c^2}=\color{red}{0}\]
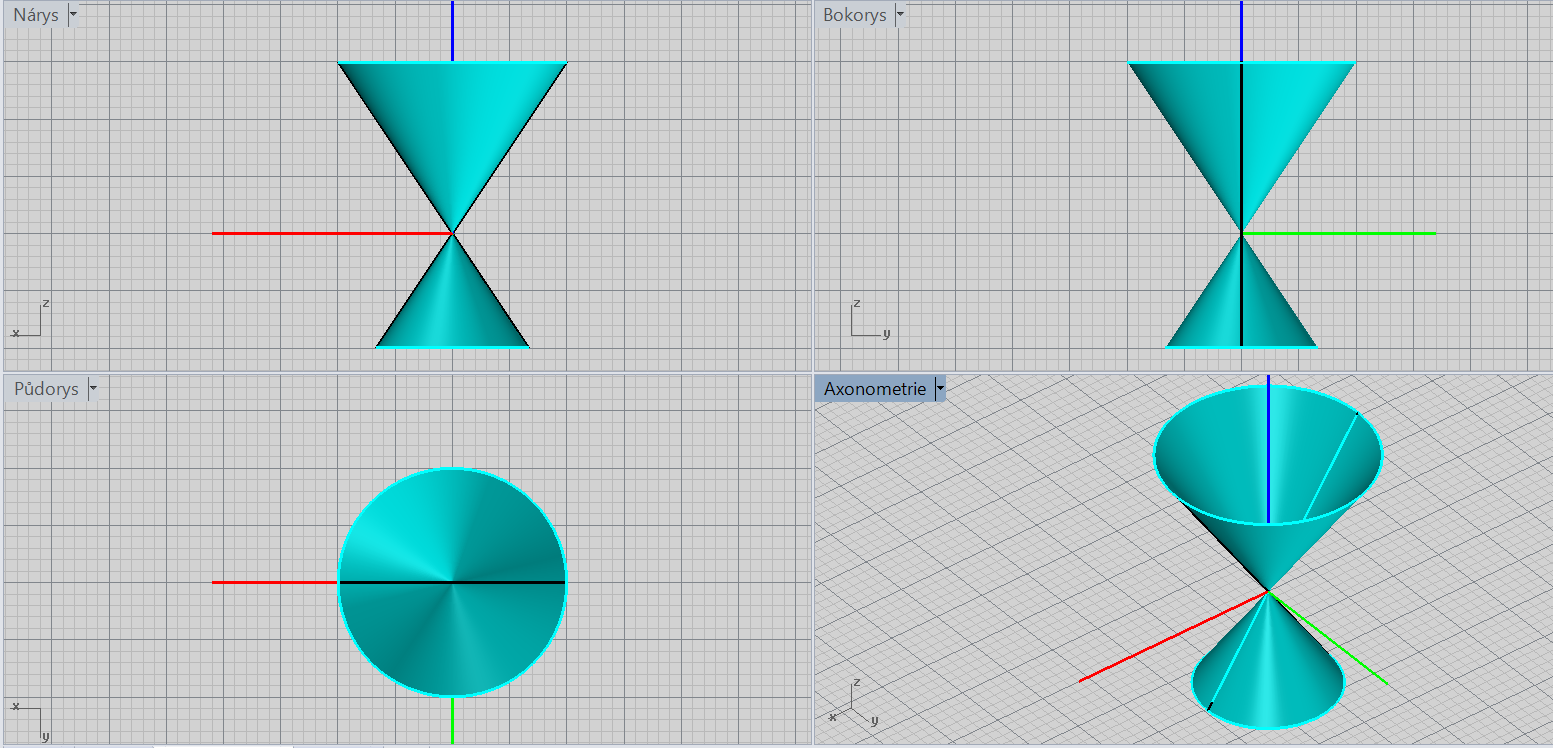
Charakteristiky: vrchol, osa rotace
skupina B-r (paraboloidy)
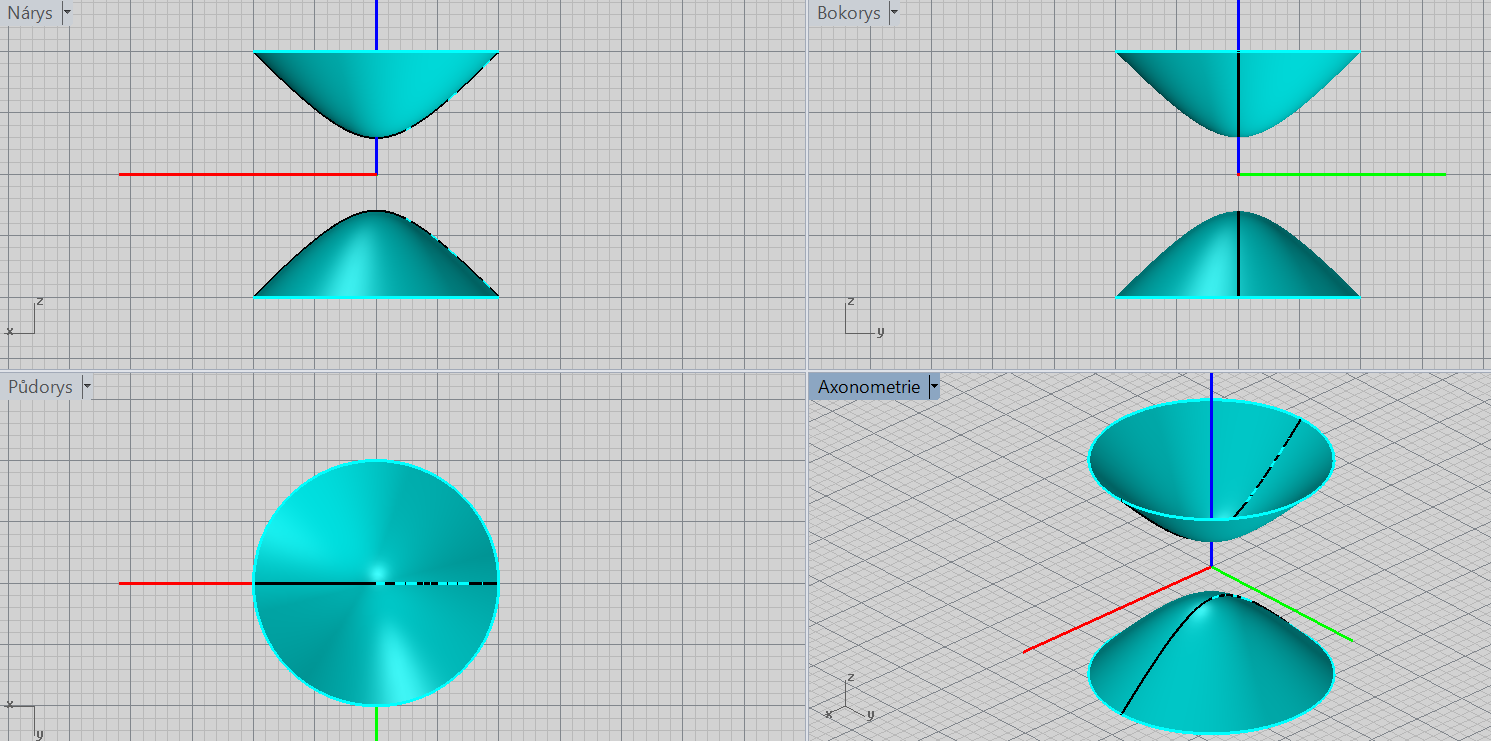
Rotační paraboloid
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{a^2}\color{red}{-}z=\color{red}{0}\]
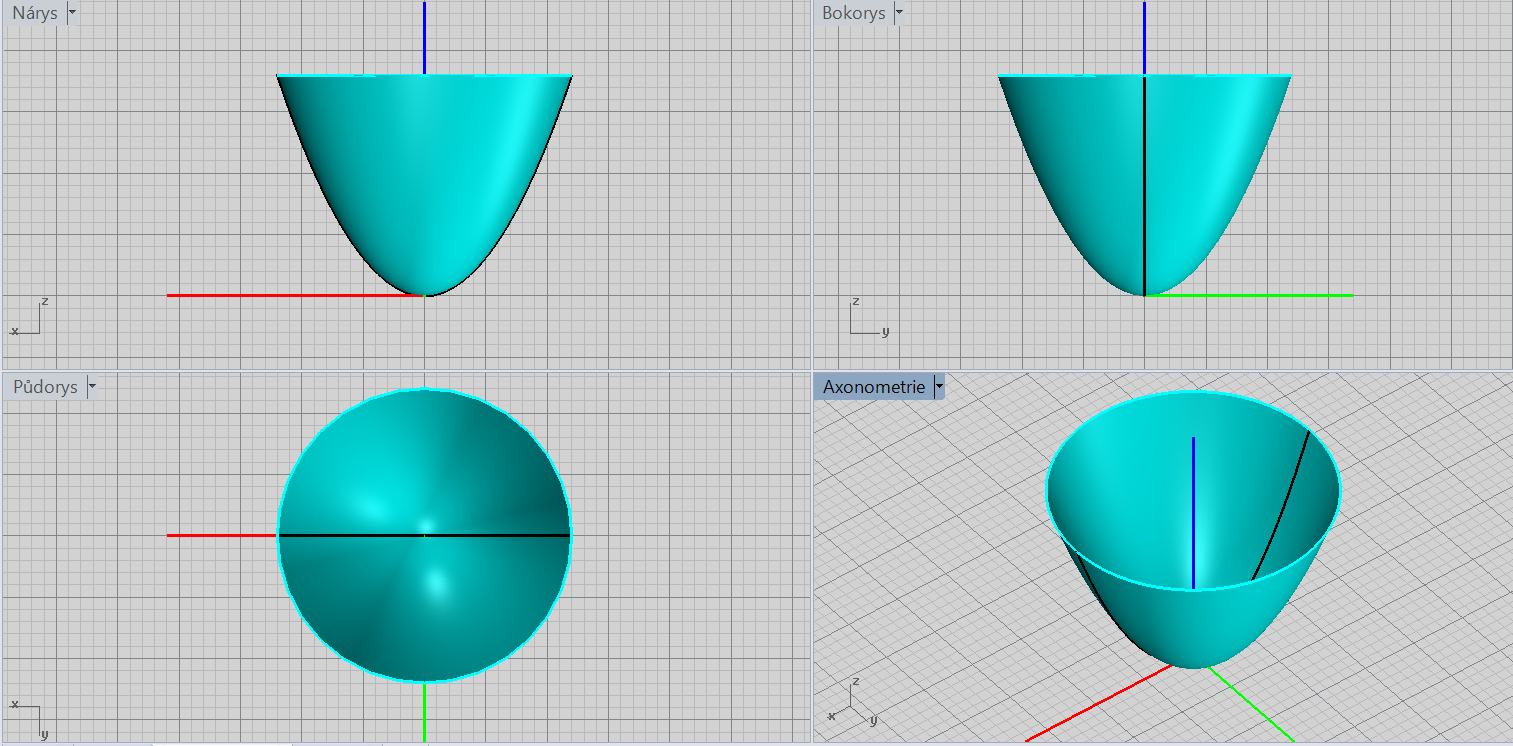
Charakteristiky: vrchol, osa rotace, orientace
Rotační paraboloid
\[\color{red}{+}\frac{x^2}{a^2}\color{red}{+}\frac{y^2}{a^2}\color{red}{+}z=\color{red}{0}\]
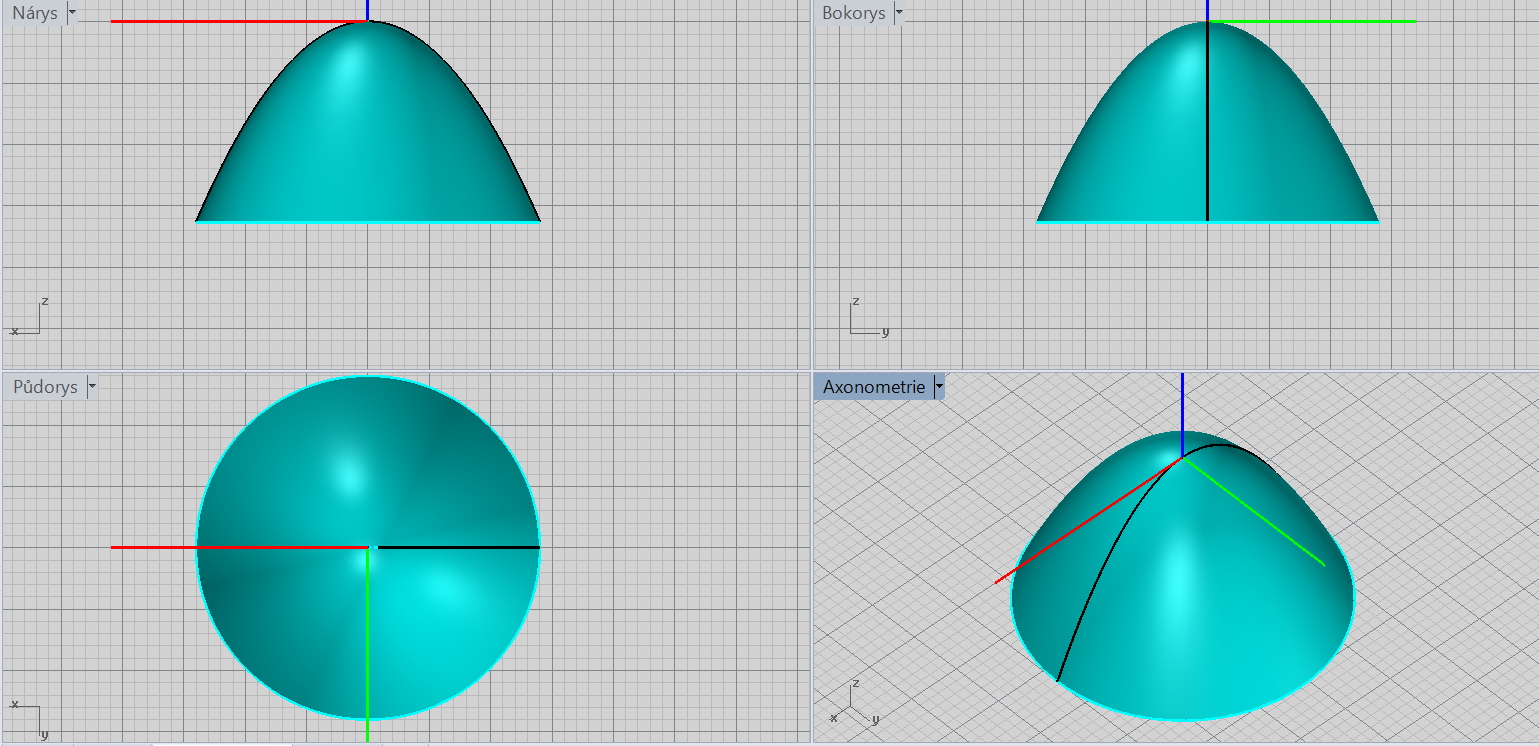
Charakteristiky: vrchol, osa rotace, orientace
skupina C-r (válcová plocha)
Rotační válcová plocha
\[\color{red}{+}\frac{x^2}{r^2}\color{red}{+}\frac{y^2}{r^2}=\color{red}{1}\]
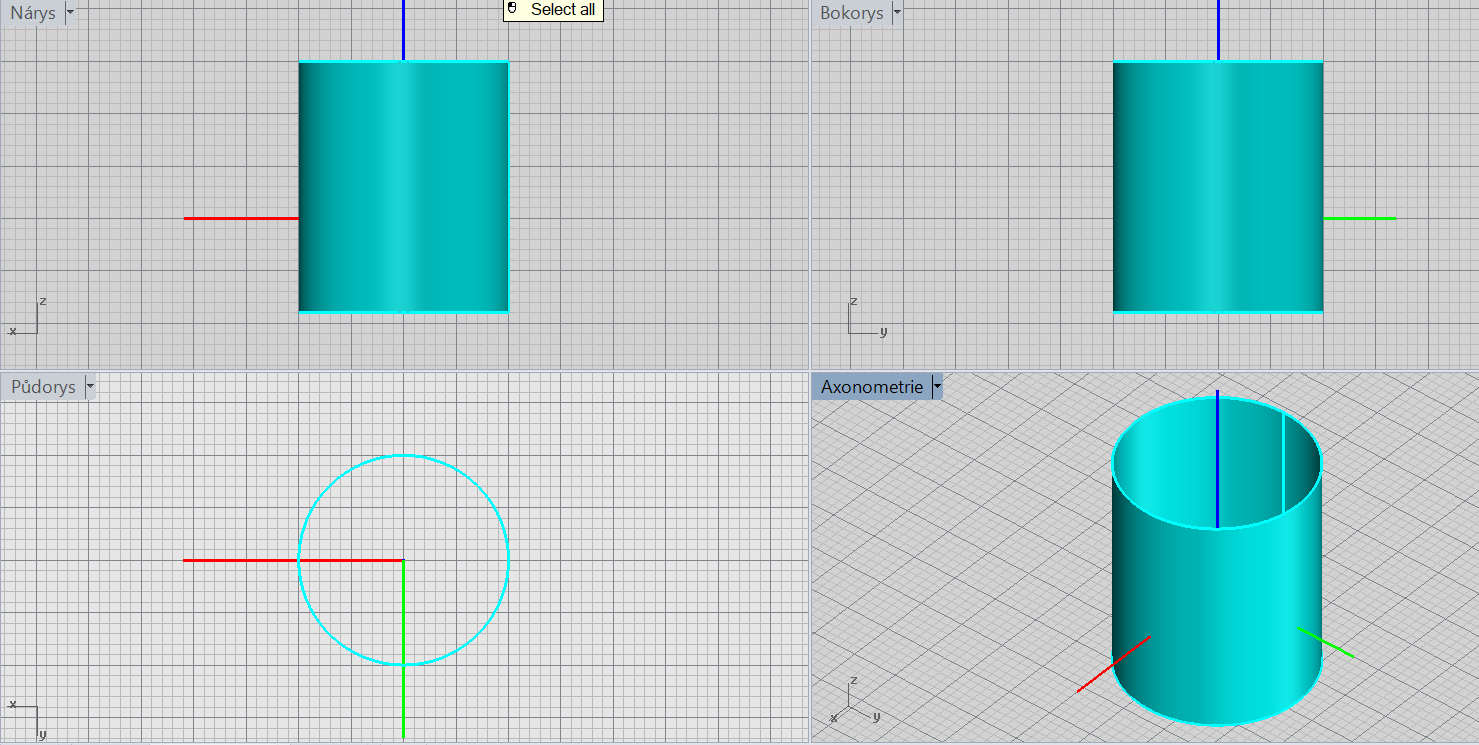
Charakteristiky: řídicí kružnice, osa rotace

Zobrazení kvadriky pomocí
sdružených průmětů

Př.2: Určete a zobrazte pomocí průmětů kvadriku
\[x^2+y^2+4y-4z^2+16z-16=0\]
úpravy rce na kanonický tvar

$x^2+y^2+4y-4z^2+16z-16=0$
$x^2+(y+2)^2-4(z^2-4z)=16+4$
$x^2+(y+2)^2-4(z-2)^2=20-16/:4$

\[\frac{x^2}{4}+\frac{(y+2)^2}{4}-(z-2)^2=1\]
\[\frac{x^2}{4}+\frac{(y+2)^2}{4}-(z-2)^2=1\]
jednodílný rotační hyperboloid

charakteristiky:
$S=[0,-2,2], o: X(t)=S+(0,0,1)t, t\in\mathbb{R}$
Křivky průmětů určit jako řezy kvadriky hlavními rovinami vedenými významným bodem kvadriky (střed/vrchol)

půdorys $$z=2 \land \frac{x^2}{4}+\frac{(y+2)^2}{4}=1$$
nárys $$y=-2 \land \frac{x^2}{4}-(z-2)^2=1$$
bokorys $$x=0 \land \frac{(y+2)^2}{4}-(z-2)^2=1$$

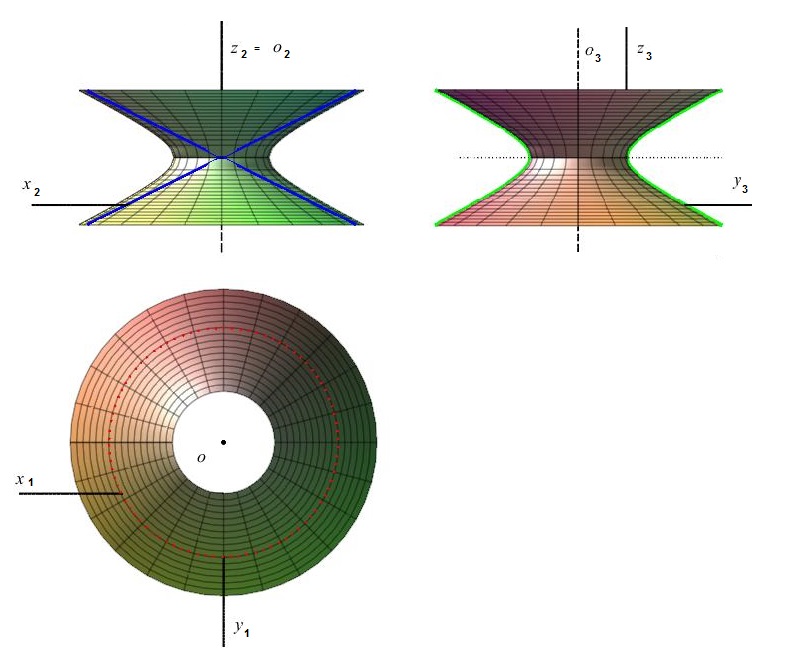
Určování průmětů kvadriky

Množina bodů v $\mathbb{E}_3$ ohraničená plochami

Př.3: Těleso je ohraničené plochami \[P: x^2+y^2-4z-12=0,\ Q: z=5-\sqrt{x^2+y^2}\] Určete hraniční plochy $P, Q$ a načrtněte sdružené průměty tělesa.
plocha $P$

$$x^2+y^2-4z-12=0$$
\[\frac{x^2}{4}+\frac{y^2}{4}-(z+3)=0\]
rotační paraboloid
vrchol $V=[0,0,-3]$, osa rotace je osa $z$, orientace $+$
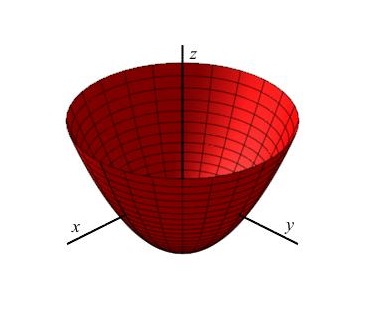
plocha $Q$
$z=5-\sqrt{x^2+y^2}$
$(z-5)=-\sqrt{x^2+y^2}/^2$

$Q': x^2+y^2-(z-5)^2=0$

$Q$ je "spodní" polovina rotační kuželové plochy $Q'$
vrchol $V=[0,0,5]$, osa rotace je osa $z$
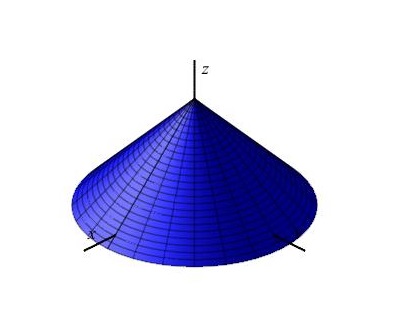
průniková křivka ploch $P,\ Q$

soustava rovnic
$(z-5)=-\sqrt{x^2+y^2}$
$x^2+y^2=4(z+3)$
$\implies (z-5)^2-4z-12=0 \Leftrightarrow (z=1 \lor z=13)$

$\implies$ kružnice $(x^2+y^2=16\land z=1)$

Těleso ohraničené plochami

Příště:

Rotační plochy