Určení pohybu - II
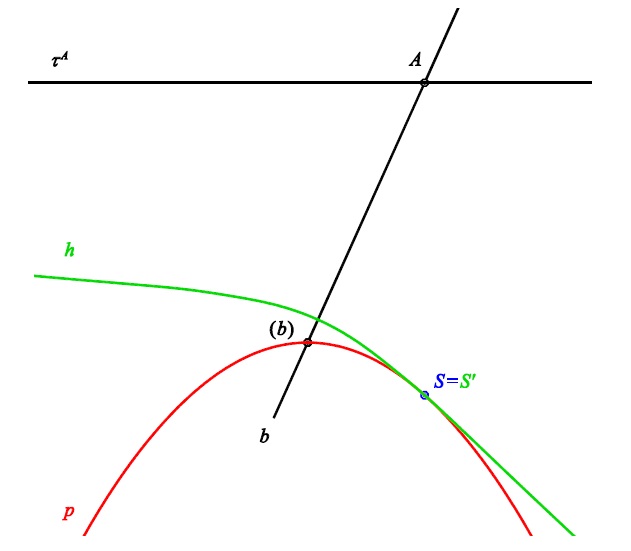
- 2 křivky - křivka $h$ v hybné soustavě, křivka $p$ v pevné soustavě
- pohyb určen odvalováním (kotálením) křivky $h$ po křivce $p$
- $p$ - pevná polodie, $h$ - hybná polodie
- při odvalování se křivky dotýkají vždy v jednom bodě (okamžitý střed otáčení)
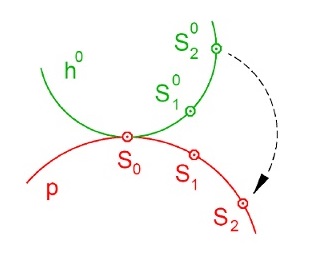
- pevná polodie: množina všech okamžitých středů otáčení (pólů pohybu)
- hybná polodie: množina všech "budoucích" okamžitých středů otáčení
- určení pohybu I ↔ II
- ukázka
Přímá konstrukce hybné polodie
Př. Sestrojte část hybné polodie pohybu určeného trajektorií bodu A a obálkou přímky p vzhledem k danému okamžiku pohybu.
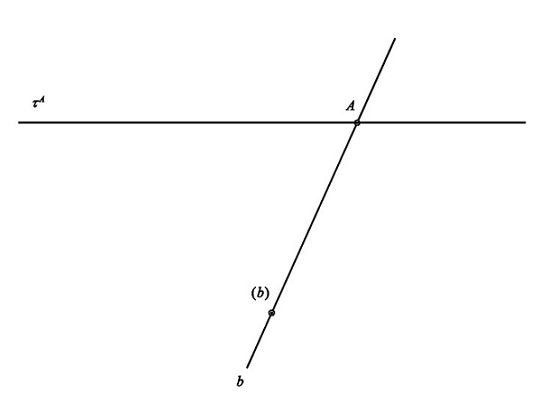
Přímá konstrukce hybné polodie
pevná polodie
Přímá konstrukce hybné polodie
přenášení středů otáčení do polohy určené daným okamžikem
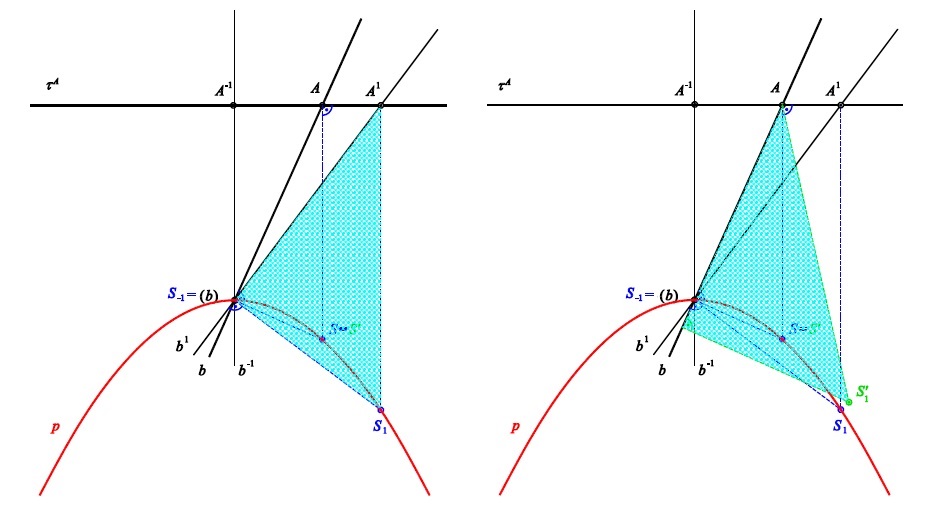
Přímá konstrukce hybné polodie
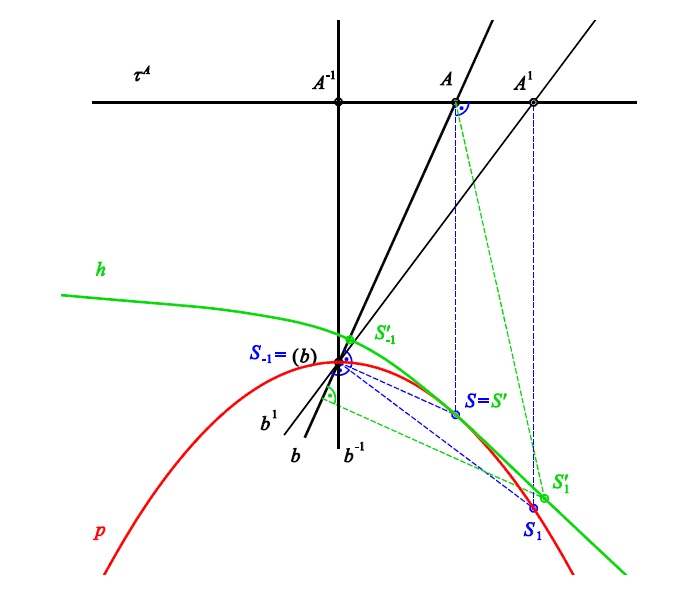
Záznam přednášky - přímá konstrukce
Konstrukce hybné polodie pomocí vratného pohybu
- záměna hybné a pevné soustavy
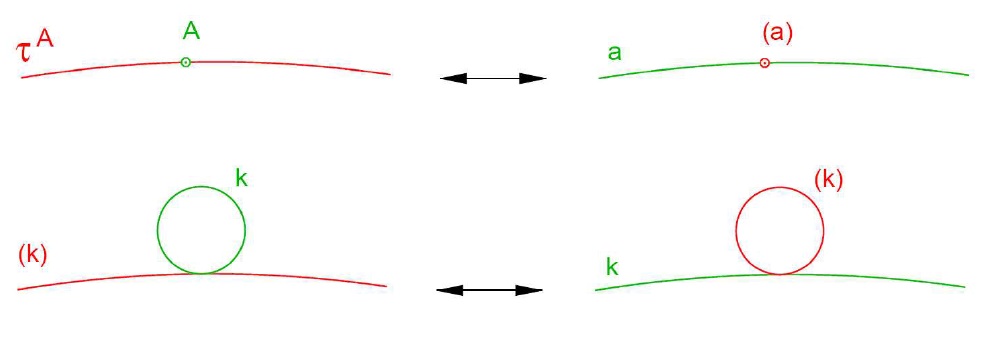
- např. kardioidický pohyb je vratný pohyb k eliptickému
pevná polodie vratného pohybu = hybná polodie pohybu výchozího
Hybná polodie - vratný pohyb
- určení vratného pohybu
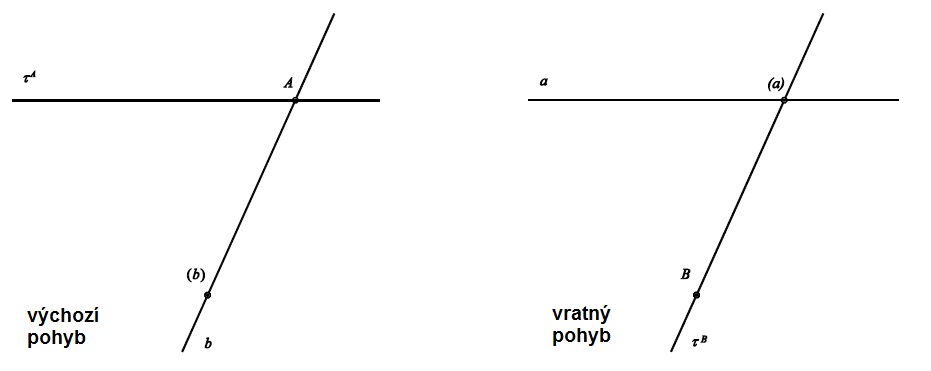
Hybná polodie - vratný pohyb
- další fáze vratného pohybu
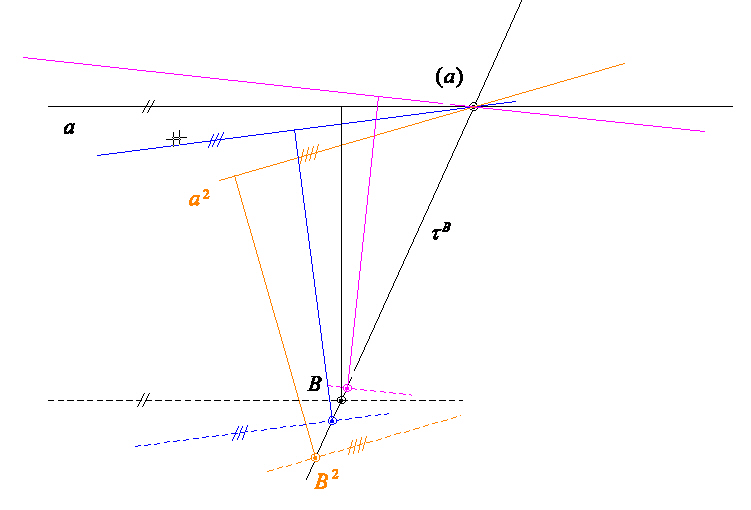
Hybná polodie - vratný pohyb
- pevná polodie vratného pohybu = hybná polodie pohybu výchozího
Záznam přednášky - vratný pohyb
Pevná a hybná polodie pohybu
Elementární pohyby v rovině určené odvalováním polodií
Cyklický pohyb:
- kružnice po přímce → cykloidální pohyb
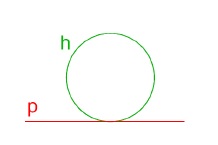
- kružnice po kružnici →
- epicykloidální pohyb
Elementární pohyby v rovině určené odvalováním polodií
Evolventní pohyb:
- přímka po kružnici → evolventní pohyb
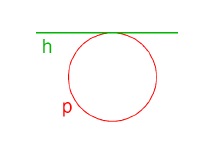
Křivky trajektorií a obálek při cyklických pohybech se nazývají cykloidy (trochoidy), při evolventním pohybu evolventy.
Cykloidy
podle polohy bodu vůči hybné polodii:
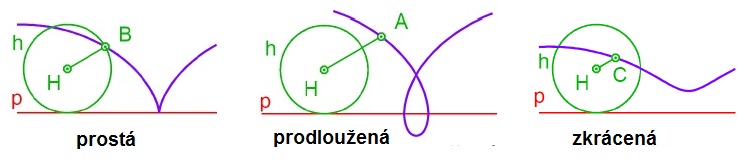
- prostá cykloida ↔ bod leží na hybné polodii
- obsahuje bod(y) vratu
- částí prosté cykloidy je tzv. křivka nejkratšího spádu - brachy(i)stochrona
- prodloužená cykloida ↔ bod leží vně hybné polodie
- obsahuje uzlový(é) bod(y)
- zkrácená cykloida ↔ bod leží uvnitř hybné polodie
- obsahuje inflexní bod(y)
Cyklické křivky - významné body
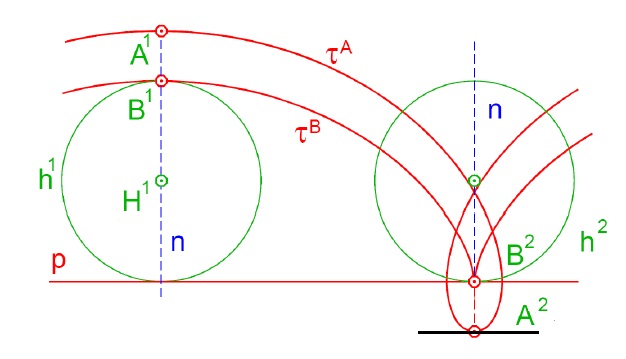
- vrchol trajektorie či obálky ↔ leží na společné normále obou polodií (= osa souměrnosti křivky), tečna je kolmá k ose souměrnosti → body $A^1, A^2$ a $B^1$
- bod vratu trajektorie či obálky ↔ leží na společné normále obou polodií, tečna s ní splývá! → bod $B^2$
Cyklické křivky - délka oblouku kružnice
- rektifikace oblouku → oblouk rozdělit na menší (nejlépe pravidelně) a ty nahradit tětivami
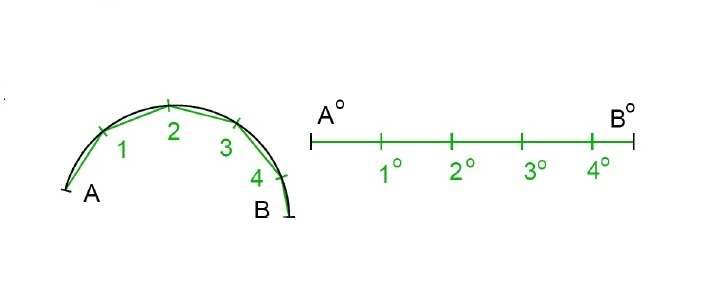
- pro známý poloměr a úhel výpočtem
- papírovým měřidlem
Příklad A - cykloidální pohyb
V daném cykloidálním pohybu sestrojte další 2 polohy kružnice $k$ včetně bodů dotyku s obálkou $(k)$.
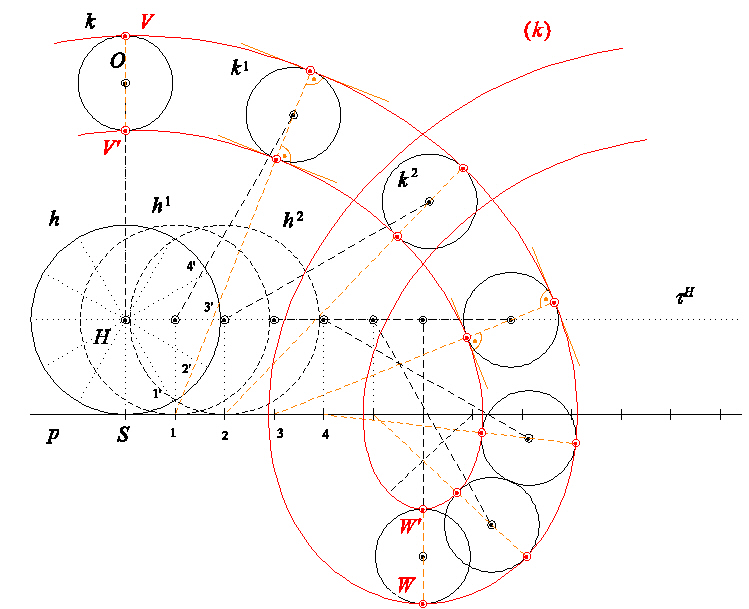
Najděte alespoň 4 vrcholy obálky $(k)$.
Najděte alespoň 4 vrcholy obálky $(k)$.
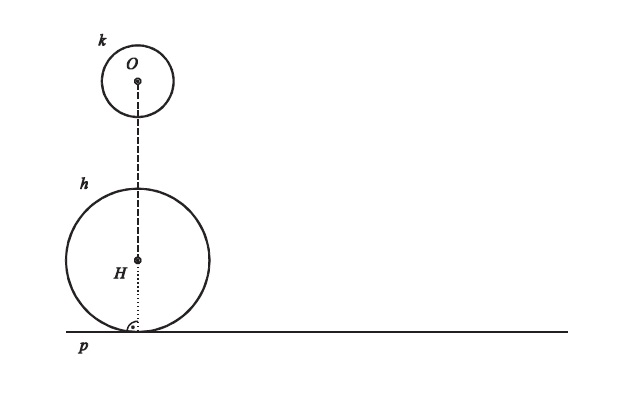
Příklad A - cykloidální pohyb
příprava - rozfázování pohybu (dělení polodií)
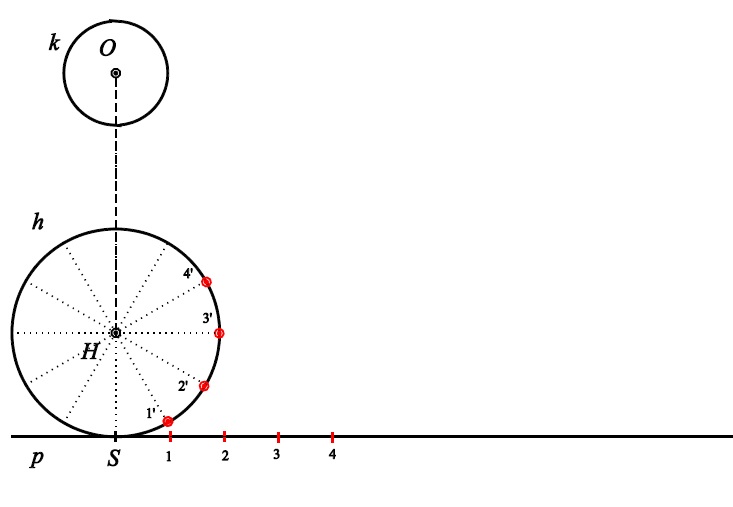
Příklad A - cykloidální pohyb
sestrojení dalších fází pohybu
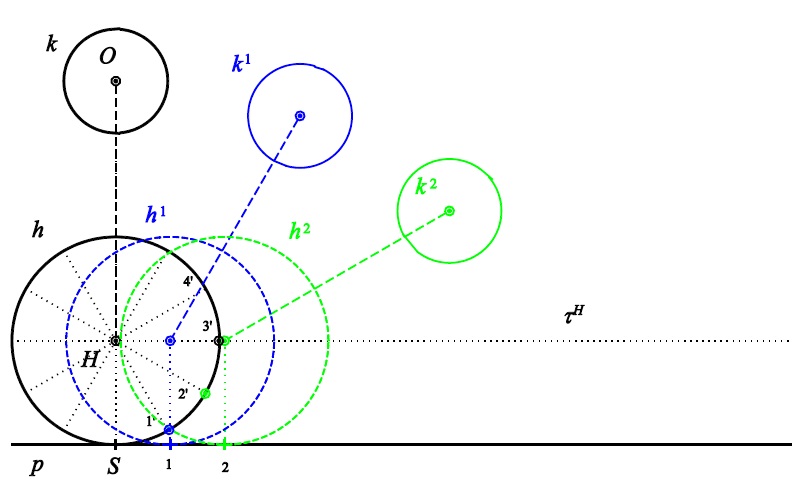
Příklad A - cykloidální pohyb
konstrukce bodů obálky
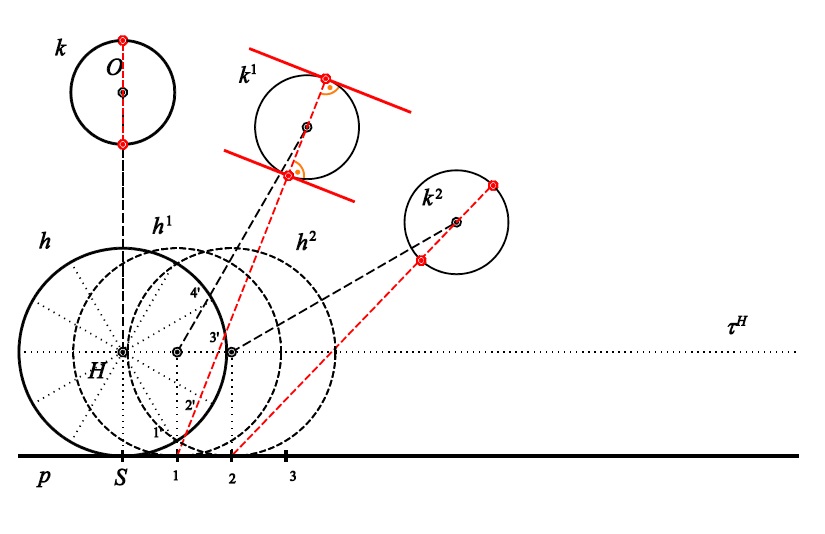
Obálka + vrcholy
Záznam přednášky - příklad A
Příklad B - evolventní pohyb
V daném evolventním pohybu sestrojte další dva body trajektorie bodu $M$, v každém z nich sestrojte tečnu k trajektorii.
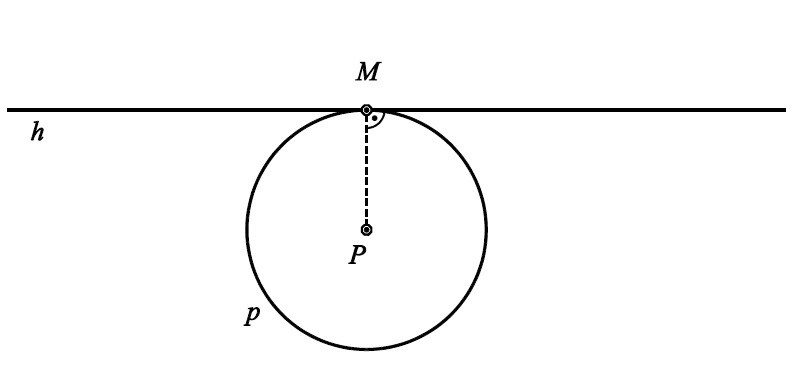
Příklad B - evolventní pohyb
rozfázování pohybu
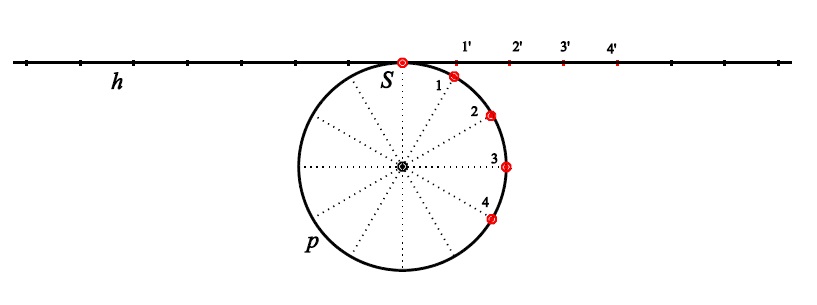
Příklad B - evolventní pohyb
sestrojení dalších fází pohybu
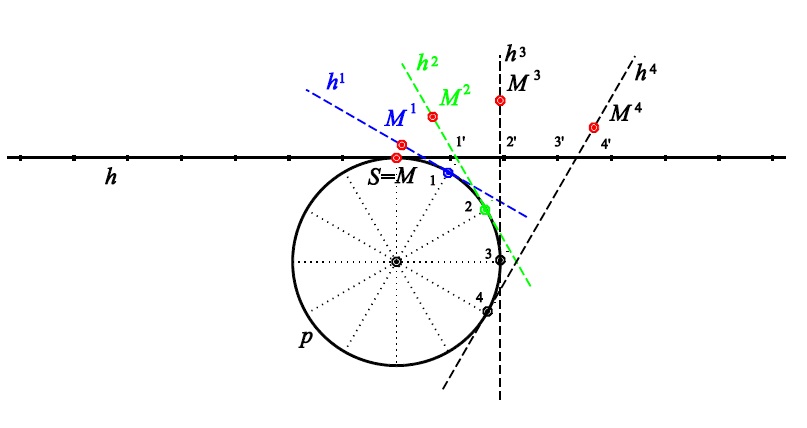
Příklad B - evolventní pohyb
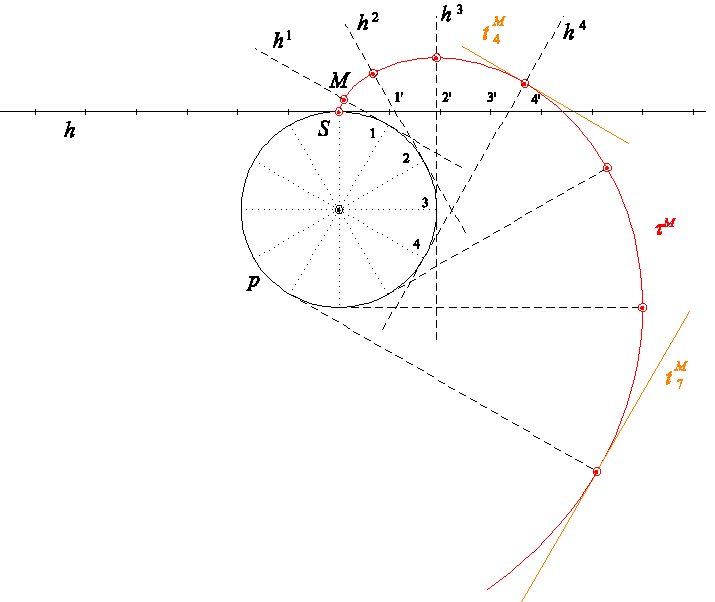
Příklad B - evolventní pohyb
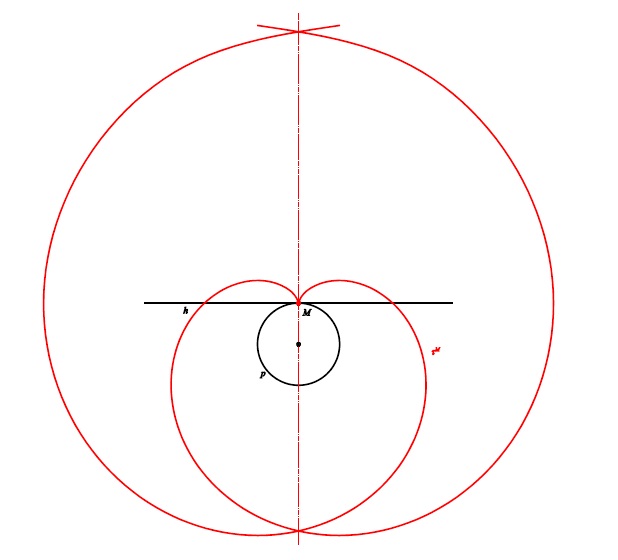
Záznam přednášky - příklad B