Konstruktivní geometrie 2023/24
Šroubovice
Šroubovice - úvod
křivka jako trajektorie bodu vykonávajícího šroubový pohyb
šroubový pohyb - pohyb složený z rotace (otáčení) a translace (posunutí),
Šroubový pohyb
Určení šroubového pohybu:
- osa šroubového pohybu
- přímá úměrnost mezi rotací a posunutím:
$$p=v_0\cdot \omega,$$
kde $p$ je posunutí, $\omega$ úhel otočení (v rad) a parametr $\color{red}{v_0}$ je tzv. redukovaná výška závitu (otočení o $1$ rad).
Pozn. Pokud je šroubovice zadaná pomocí tzv. výšky závitu $\color{red}v$ (otočení o $2\pi$ rad), pak: \[v_0=\frac{v}{2\pi}\] - smysl šroubového pohybu
- pravotočivý ( = stoupání podle pravidla pravé ruky, rotace proti směru hodin) nebo levotočivý
šroubovice - určení
bod, šroubový pohyb (osa, parametr $v_0$ nebo výška závitu, smysl)
šroubovice - rovnice
bod $A[x_0,y_0,0]$, šroubový pohyb - osa $z$, parametr $v_0$, pravotočivý
rotace $\rightarrow$ kružnice $$P_k(t)=(\sqrt{x_0^2+y_0^2}\cos t,\sqrt{x_0^2+y_0^2}\sin t,0), t\in<0,2\pi>$$
translace $\rightarrow$ přímka $$P_p(t)=(x_0,y_0,t),t\in\mathbb{R}$$
šroubový pohyb $\rightarrow$ šroubovice $$P(t)=(r\cos t,r\sin t,v_0t), t\in\mathbb{R}, r=\sqrt{x_0^2+y_0^2}$$
(vzdálenost $r$ určujícího bodu od osy šroubového pohybu je tzv. poloměr šroubovice).
Šroubovice - zobrazení
v Mongeově promítání:
- rotace $\rightarrow$ kružnice ... v rovině kolmé k ose šroubového pohybu
- posunutí $\rightarrow$ přímka ... rovnoběžná s osou šroubového pohybu
Úmluva:
- osa šroubového pohybu kolmá k půdorysně
- ve 2. průmětu vyznačit šipkou dolů klesání + v 1. průmětu vyznačit šipkou smysl klesání

- parametr $v_0$ vyznačen úsečkou na ose $o$
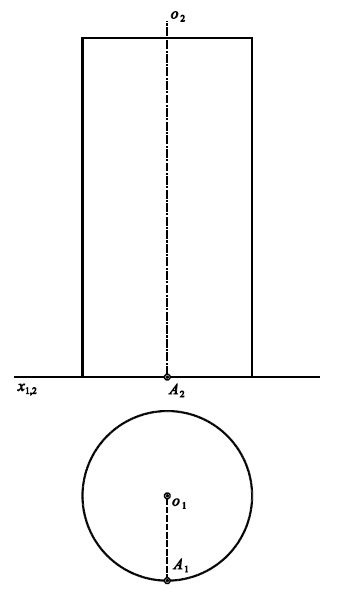
Příklad 1: Zobrazte jeden závit pravotočivé šroubovice bodu $A$ na válcové ploše.
Šroubový pohyb je určen osou $o$, výška závitu = výška zobrazené části válcové plochy.
Šroubový pohyb je určen osou $o$, výška závitu = výška zobrazené části válcové plochy.

Základní úlohy o šroubovicích
dáno: bod, šroubový pohyb (osa $o$, parametr $v_0$, smysl)
- konstrukce dalšího bodu šroubovice, je-li daný úhel otočení (graficky) při šroubovém pohybu
- konstrukce dalšího bodu šroubovice, je-li dané posunutí při šroubovém pohybu
- konstrukce tečny v libovolném bodě šroubovice
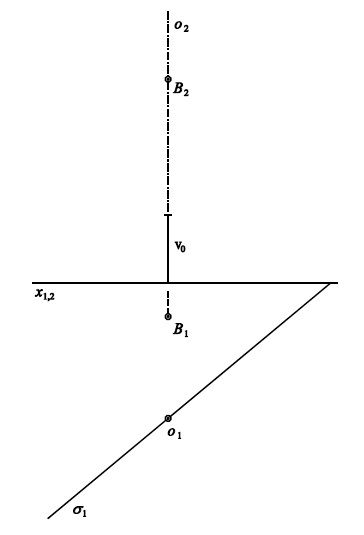
Příklad 2: Levotočivý šroubový pohyb je určen osou $o$ a parametrem $v_0$.
Sestrojte průsečík $R$ šroubovice bodu $B$ s rovinou $\sigma$.
Sestrojte průsečík $R$ šroubovice bodu $B$ s rovinou $\sigma$.
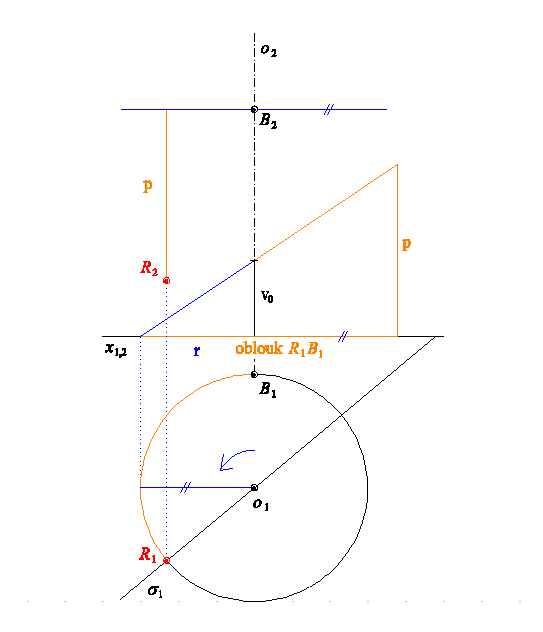
Příklad 3: Pravotočivý šroubový pohyb je určen osou $o$ a parametrem $v_0$.
Sestrojte průsečík $R$ šroubovice bodu $B$ s rovinou $\sigma$.
Sestrojte průsečík $R$ šroubovice bodu $B$ s rovinou $\sigma$.

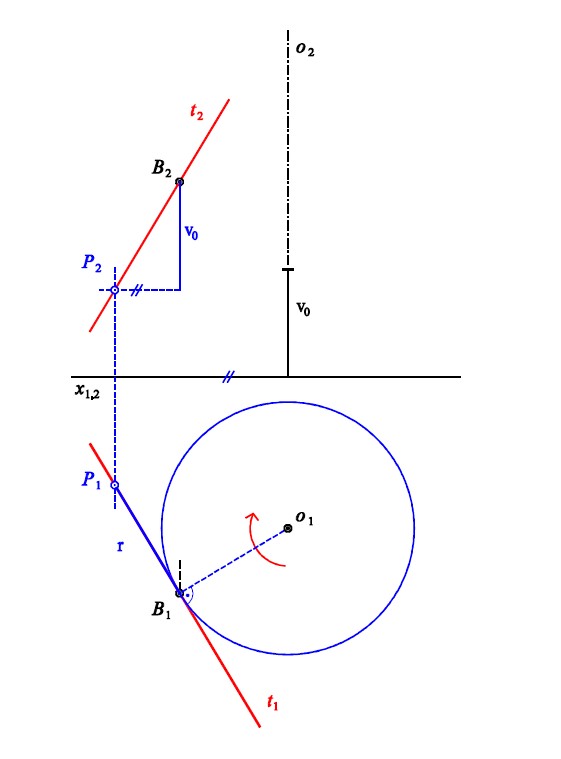
Tečna ke šroubovici
tečna prostorové křivky:
- analyticky $\rightarrow$ přímka určená bodem a tečným vektorem $P'$ v bodě křivky \[P'(t)=(-r\sin t, r\cos t,v_0)\]
- graficky $\rightarrow$ průmět tečny ke křivce = tečna k průmětu křivky
- půdorys tečny $\Rightarrow$ tečna ke kružnici
- nárys tečny $\Rightarrow$ tečna k nárysu šroubovice ... ?
Řídící kužel šroubovice
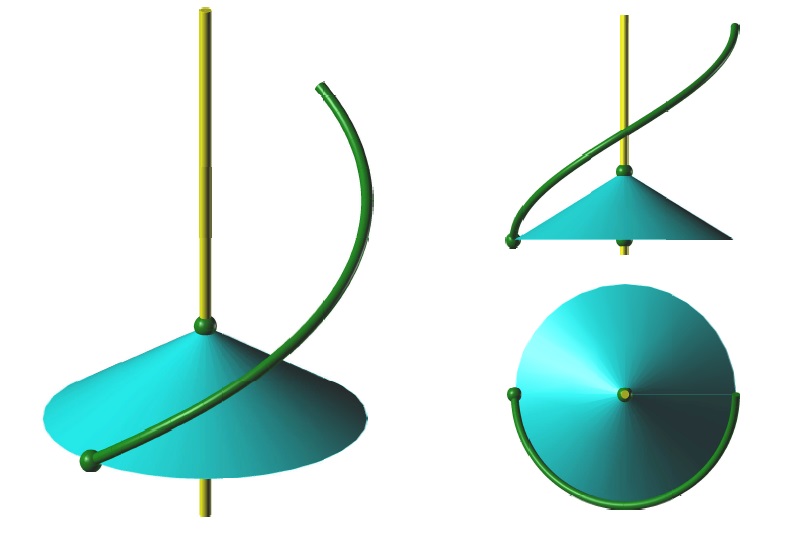
Řídící kužel šroubovice je rotační kužel s osou v ose šroubového pohybu,
vrcholem ve výšce $v_0$ a poloměrem kružnice podstavy totožným s poloměrem šroubovice.
Tečna šroubovice
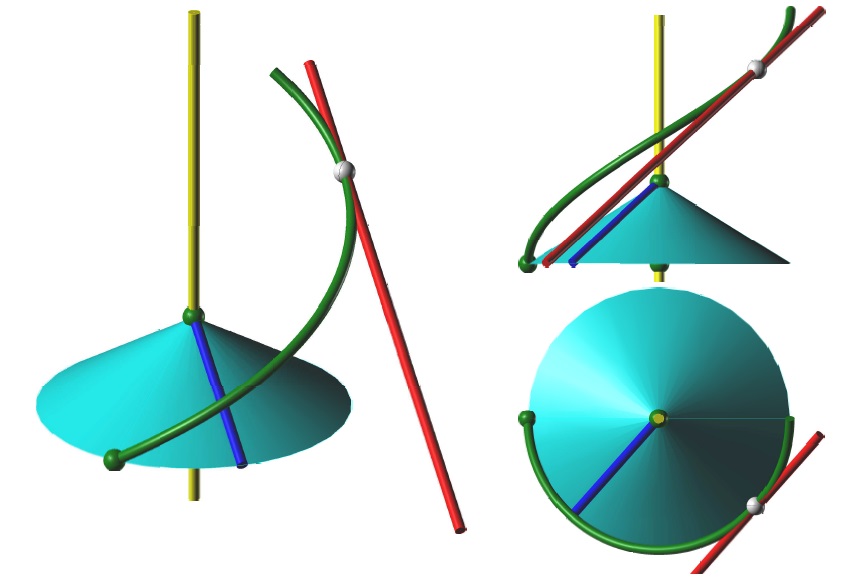
Tečna ke šroubovici v každém jejím bodě je rovnoběžná s jednou povrchovou přímkou řídícího kužele dané šroubovice.
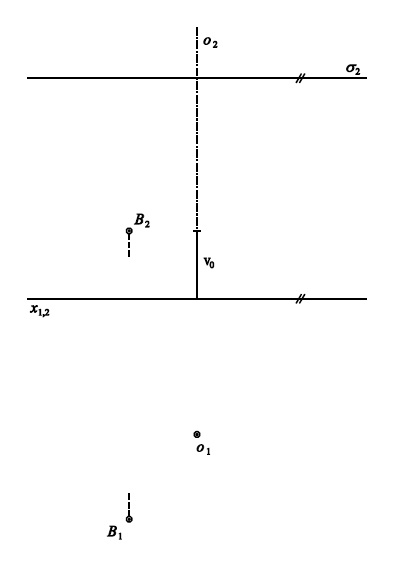
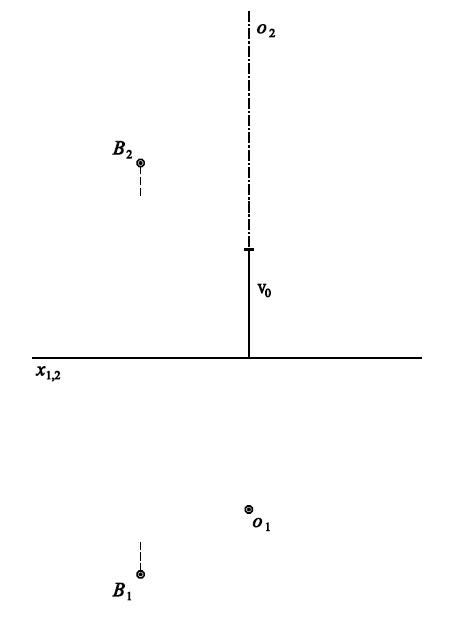
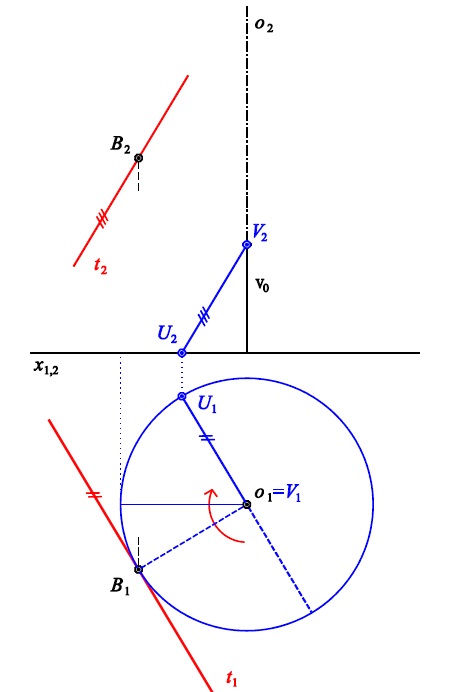
Příklad 4: Pravotočivý šroubový pohyb je určen osou $o$ a parametrem $v_0$.
V bodě $B$ sestrojte tečnu $t$ ke šroubovici bodu $B$.
V bodě $B$ sestrojte tečnu $t$ ke šroubovici bodu $B$.
příště: