Konstruktivní geometrie 2023/24
Rozvinutelné přechodové plochy
Přechodová plocha

- hladká rozvinutelná plocha mezi dvěma rovinnými křivkami (profily)
- složená z hladce na sebe navazujících segmentů rozvinutelných ploch
- konstrukce jednotlivých segmentů závisí na vzájemné poloze rovin profilových křivek
křivky v navzájem rovnoběžných rovinách
dvě hladké křivky
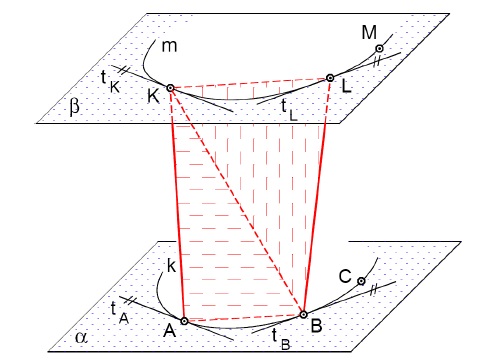
Postup:
- povrchovou přímkou spojit body s rovnoběžnými tečnami: $AK$, $BL$
- prostorové čtyřúhelníky mezi dvěma površkami nahradit dvěma trojúhelníky: $ABLK \rightarrow ABK$, $BLK$
- rozvinutí sestrojit jako síť z trojúhelníků
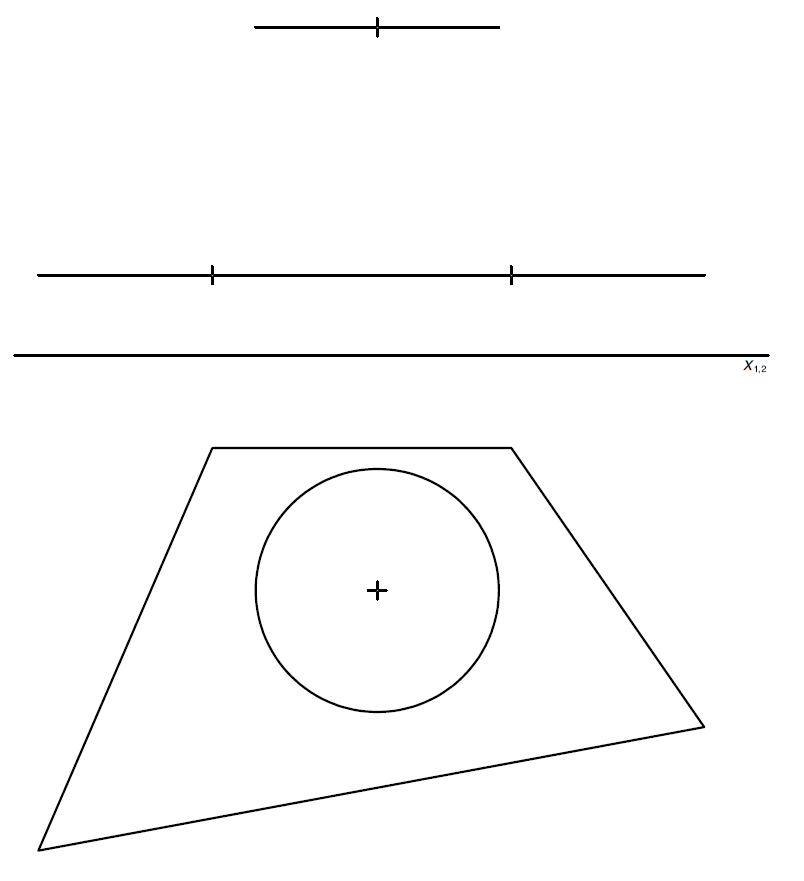
Příklad 1: Zobrazte rozvinutelnou přechodovou plochu mezi dvěma křivkami $k$ a $k'$. Plochu rozviňte.
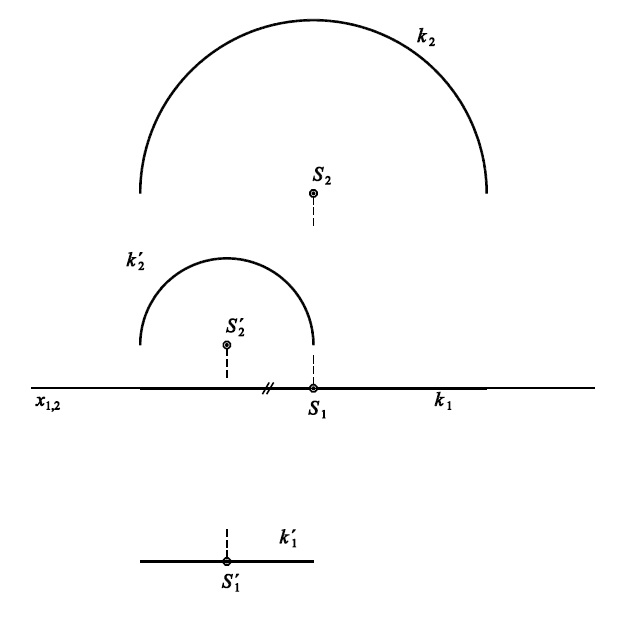
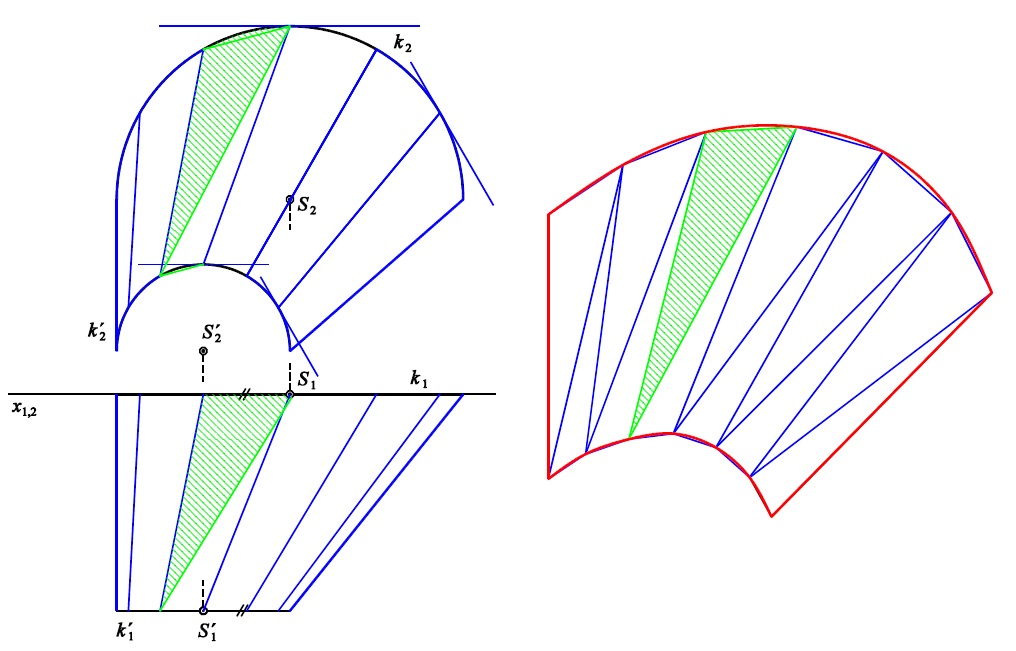
hladká křivka a lomená čára
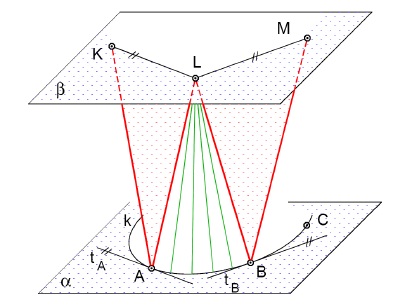
Postup:
- povrchové přímky bodů s rovnoběžnými tečnami vytvoří segmenty rovin: $ALK$, $BML$
- doplnit částmi kuželových ploch: $LAB$
- rozvinutí sestrojit jako trojúhelníkovou síť
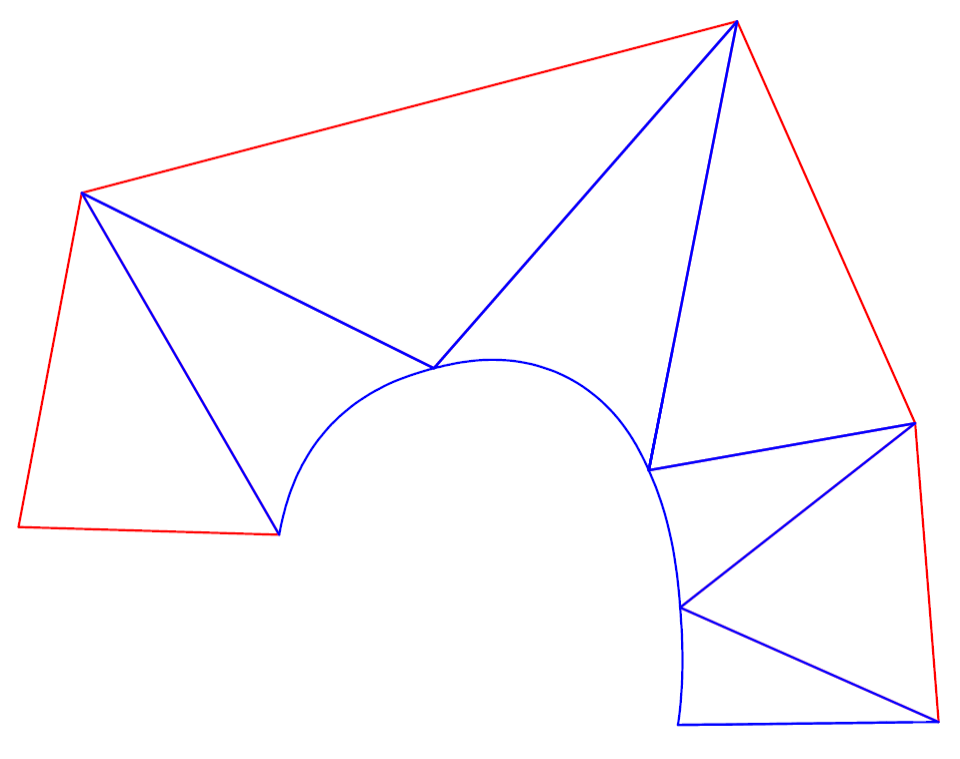
Příklad 2: Zobrazte rozvinutelnou přechodovou plochu mezi křivkou $k$ a lomenou čarou. Plochu rozviňte.
křivky v navzájem různoběžných rovinách
dvě hladké křivky
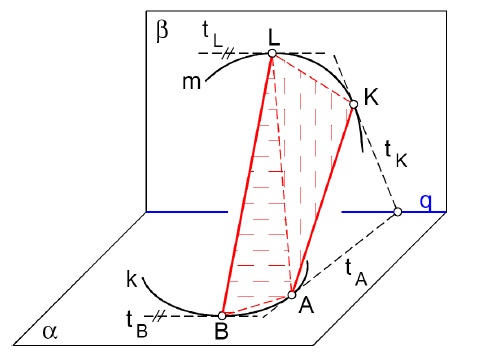
Postup:
- povrchové přímky spojují body, jejichž tečny ke křivkám se protínají na průsečnici rovin: $BL$, $AK$
- prostorové čtyřúhelníky mezi dvěma površkami nahradit dvěma trojúhelníky: $BAKL \rightarrow BAL$, $AKL$
- rozvinutí sestrojit jako síť z trojúhelníků
Více info např. na mathcurve.com
hladká křivka a lomená čára
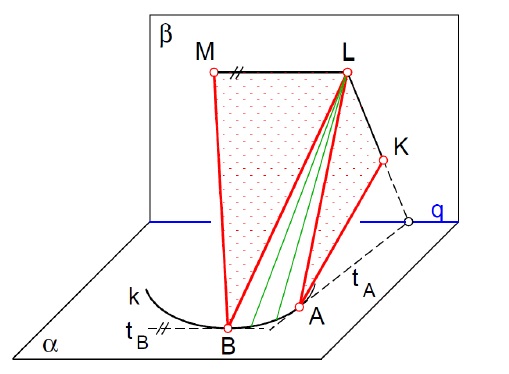
Postup:
- povrchové přímky spojují body, jejichž tečny se protínají na průsečnici rovin $\rightarrow$ trojúhelníky rovin: $AKL$, $BLM$
- doplnit částmi kuželových ploch: $LAB$
- rozvinutí sestrojit jako síť z trojúhelníků
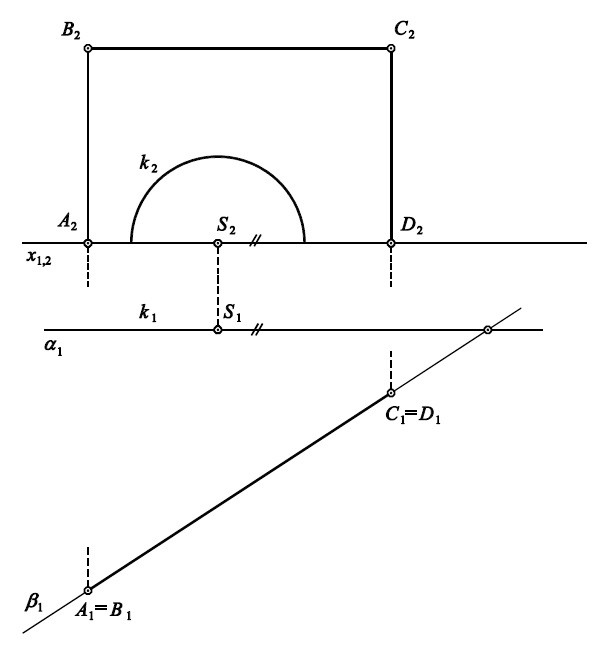
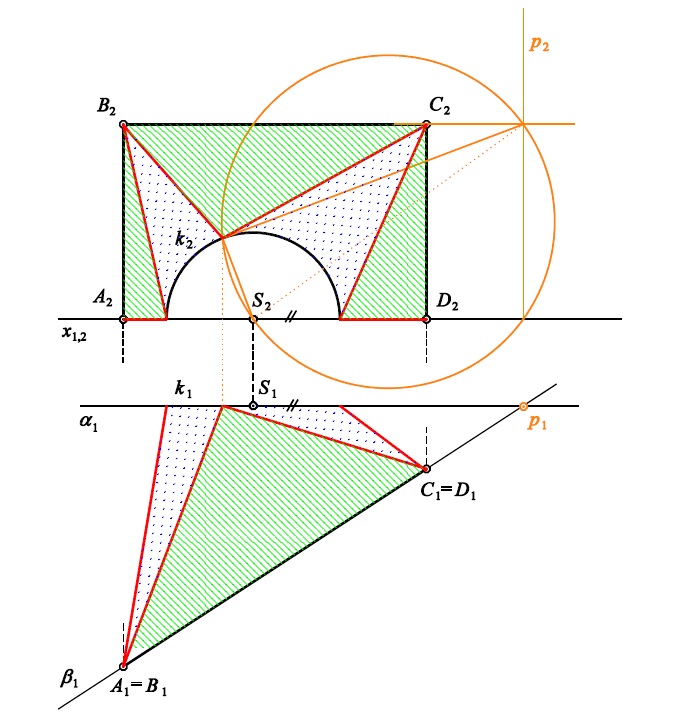
Příklad 3: V Mongeově promítání zobrazte přechodovou rozvinutelnou plochu mezi půlkružnicí $k$ v rovině $\alpha$ a lomenou čarou $ABCD$ v rovině $\beta$.
příště: